https://x.com/elonmusk/status/2003165966243598738?s=20

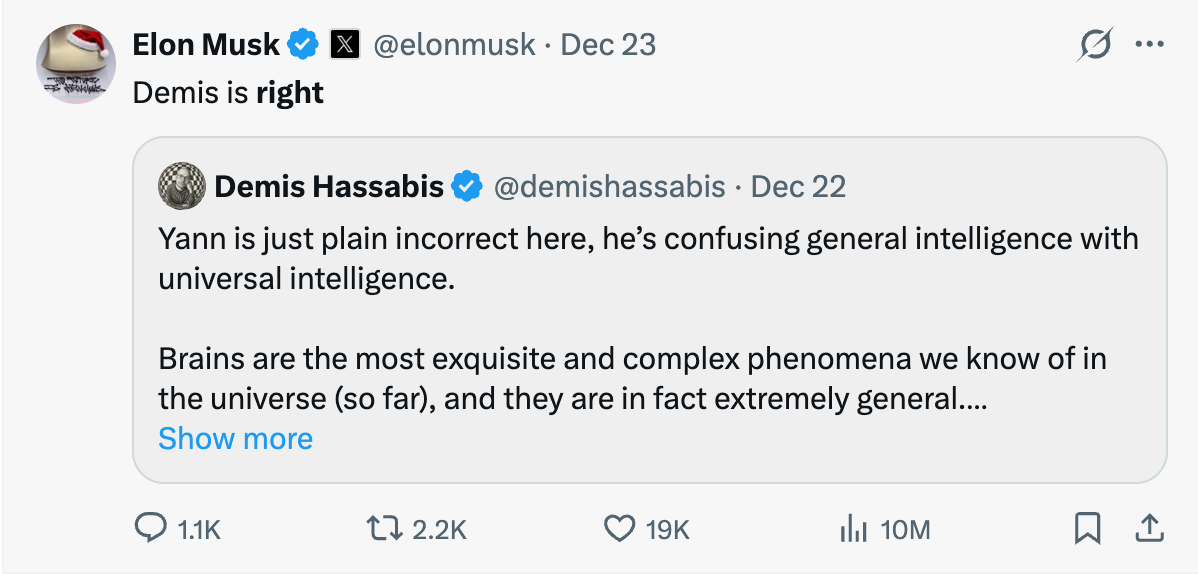
Yann is just plain incorrect here, he’s confusing general intelligence with universal intelligence. Brains are the most exquis​ite and complex phenomena we know of in the universe (so far), and they are in fact extremely general. Obviously one can’t circumvent the no free lunch theorem so in a practical and finite system there always has to be some degree of specialisation around the ​target distribution that is being learnt. But the point about generality is that in theory, in the Turing Machine sense​, the architecture of ​s​uch a general system is capable of learning anything computable given enough time and memory​ (and data), and the human brain (and AI foundation models) are approximate Turing Machines. Finally, with ​regards to ​Yann's comments about chess players, it’s amazing that humans could have invented chess ​in the first place (and all the other ​a​spects ​o​f modern civilization ​from science to 747s!) let alone get as brilliant at it as someone like Magnus. He may not be ​strictly optimal (after all he has finite memory and limited time to make a decision) but it’s incredible what he and we can do with our brains given they were evolved for hunter gathering.

————————————————————

杨立昆在这里完全错了，他把通用智能和全能智能搞混了。大脑是我们迄今所知宇宙中最精妙复杂的现象（目前为止），实际上具有极强的通用性。显然我们无法绕过"没有免费午餐"定理，因此在实用且有限的系统中，针对目标学习分布总需要某种程度的专门化设计。但通用性的核心在于：从图灵机的理论层面来看，这类通用系统架构只要有足够时间、内存（和数据），就能学会任何可计算任务——人脑（和AI基础模型）正是近似图灵机。最后关于杨立昆对棋手的评论：人类能发明国际象棋本身已是奇迹（更不用说创造从科学到波音747的现代文明所有成就！），像芒努斯这样的棋王能达到如此高超境界更令人惊叹。他或许达不到严格意义上的最优解（毕竟受限于记忆容量和决策时间），但考虑到我们大脑是为狩猎采集进化而来的，他和人类能用大脑达到的成就实在不可思议。

这段话的来源是对 

https://x.com/i/status/2000959102940291456

杨立昆在这里的演讲的评价。

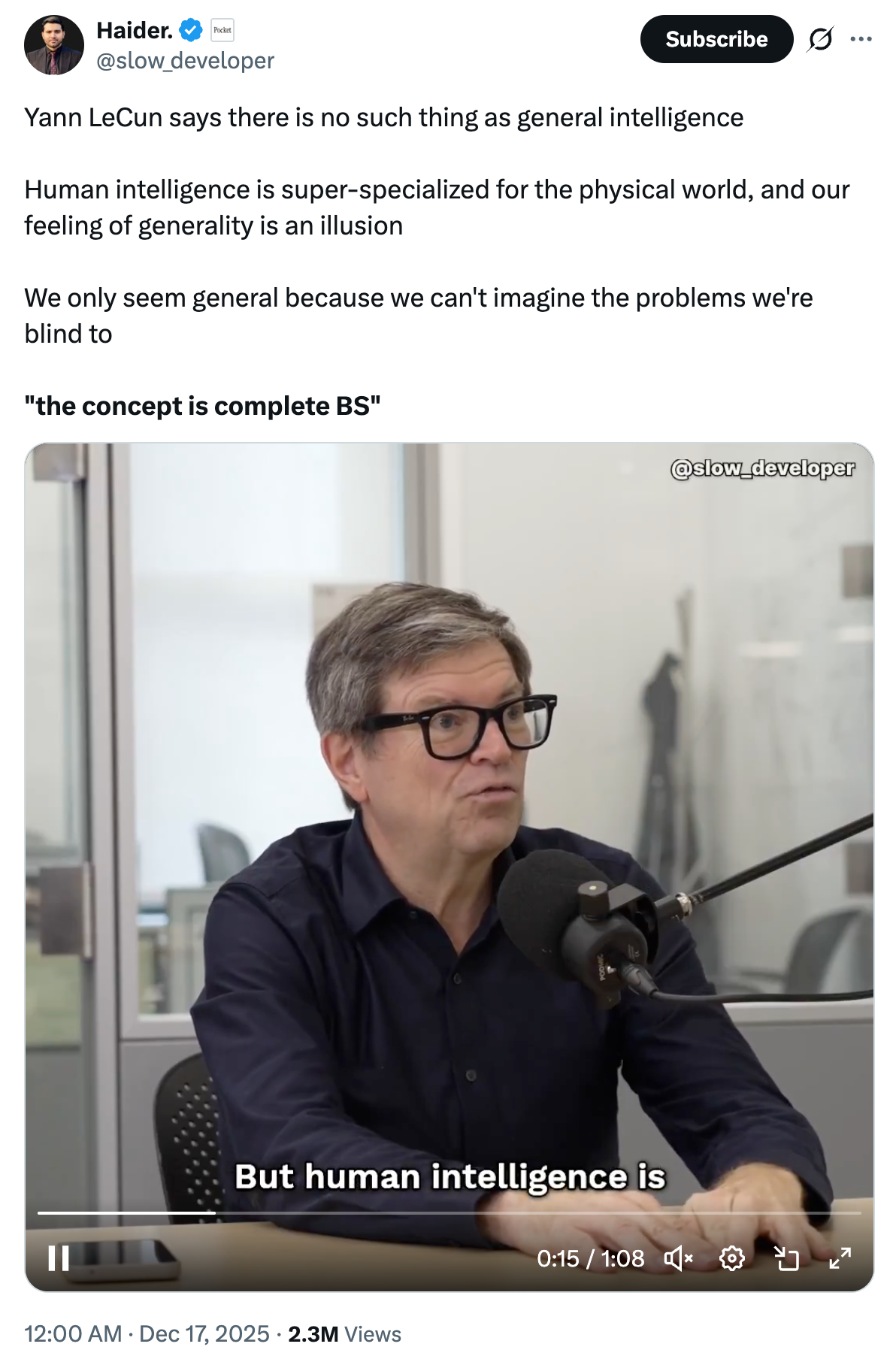
Yann LeCun says there is no such thing as general intelligence Human intelligence is super-specialized for the physical world, and our feeling of generality is an illusion We only seem general because we can't imagine the problems we're blind to

"the concept is complete BS"

————————————————————

杨立昆表示，通用智能根本不存在。人类智能是专门为物理世界高度特化的，我们感受到的通用性只是错觉。"我们看似具备通用性，仅仅是因为无法想象自己认知盲区里的问题——这个概念纯属胡扯"

FROM： https://x.com/slow_developer/status/2000959102940291456?s=20

杨立昆显然对此有自己的看法

I think the disagreement is largely one of vocabulary. I object to the use of "general" to designate "human level" because humans are extremely specialized. You may disagree that the human mind is specialized, but it really is. It's not just a question of theoretical power but also a question of practical efficiency. Clearly, a properly trained human brain with an infinite supply of pens and paper is Turing complete. But for the vast majority of computational problems, it's horribly inefficient, which makes it highly suboptimal under bounded resources (like playing a chess game). Let me give an analogy: in theory, a 2-layer neural net can approximate any function as close as you want. In practice, almost every interesting function requires a impractically large number of units in the hidden layer. So we use multi-layer networks (that's actually the raison d'être for deep learning). Here is another argument: the optic nerve has 1 million nerve fiber. Let's make the simplifying assumption that the signals are binary. A vision task is therefore a boolean function from 1E6 bits to 1 bit. Among all the possible such functions, what proportion are implementable by the brain? The answer is: an infinitesimal proportion. The number of boolean functions of 1 million bits is 2^(2^1E6), which an unimaginably large number, about 2^(1E301030) or 10^(3x1E301029). Now, assuming that the human brain has 1E11 neurons, and perhaps 1E14 synapses, each represented on, say, 32 bits. The total number of bits to specify the entire connectome is at most 3.2E15. This means the total number of boolean function representable (computable) by the entire human brain is at most 2^(3.2E15). This is a teeny-tiny number compared to 2^(1E301030). Not only are we not general, we are *ridiculously* specialized. The space of possible function is vast. We don't realize it because most of those functions are unfathomably complicated to and us and look completely random. I love this quote from Albert Einstein: "the most incomprehensible thing about the world is that the world is comprehensible" It's pretty incredible that among all the random ways the world could be organized, we can actually find a way to understand a tiny part of it. The part we don't understand, we call entropy. Most of the information content of the universe is entropy: things we simply cannot understand with our feeble minds and choose to ignore.

————————————————————————————

我认为分歧主要在于词汇使用。我反对用"通用"来指代"人类水平"，因为人类其实是高度特化的。你或许不认同人脑具有特化性，但它确实如此。这不仅关乎理论能力，更涉及实际效率问题。显然，配备无限纸笔的经过训练的人脑具备图灵完备性。但对于绝大多数计算问题而言，其效率极其低下，在资源受限情况下（比如下棋时）表现极差。让我做个类比：理论上双层神经网络可以无限逼近任何函数，但实际上几乎所有有意义的函数都需要隐藏层包含不切实际的大量神经元，因此我们才使用多层网络（这正是深度学习存在的根本原因）。再举一例：视神经含有百万级神经纤维。假设信号是二进制的，那么视觉任务就是从1E6比特到1比特的布尔函数。在所有可能函数中，大脑能实现的比例是多少？答案是：无限趋近于零。百万比特布尔函数的总数是2^(2^1E6)，这个难以想象的数字约等于2^(1E301030)或10^(3x1E301029)。假设人脑有1E11个神经元和约1E14个突触，每个用32比特表示，那么描述整个连接组最多需要3.2E15比特。这意味着人脑可表示（计算）的布尔函数总数上限是2^(3.2E15)，与2^(1E301030)相比简直微不足道。我们不仅不通用，而且是荒谬地特化。可能函数的空间浩瀚无垠，我们之所以意识不到这点，是因为其中绝大多数函数对我们来说复杂得难以理解且完全随机。爱因斯坦有句名言深得我心："世界最不可理解之处，就在于它居然可以被理解。"在所有可能的随机世界构成方式中，我们竟能理解其中微小部分，这着实不可思议。无法理解的部分，我们称之为熵。宇宙中大部分信息内容都是熵——那是我们脆弱心智无法理解而选择忽略的存在。

FROM： https://x.com/ylecun/status/2003227257587007712?s=20

有人整理了他们的关键点差异：

https://x.com/DenisLabelle/status/2003173626984468610?s=20