Basic statistics - 14. The repeated-measures ANOVA | explained with a simple example
The。
14. The repeated-measures ANOVA | explained with a simple example
one-way ANOVA vs repeated-measures ANOVA
The difference from the one-way ANOVA is that the denominator is repeated-measures ANOVA does not include the variance between the subjects.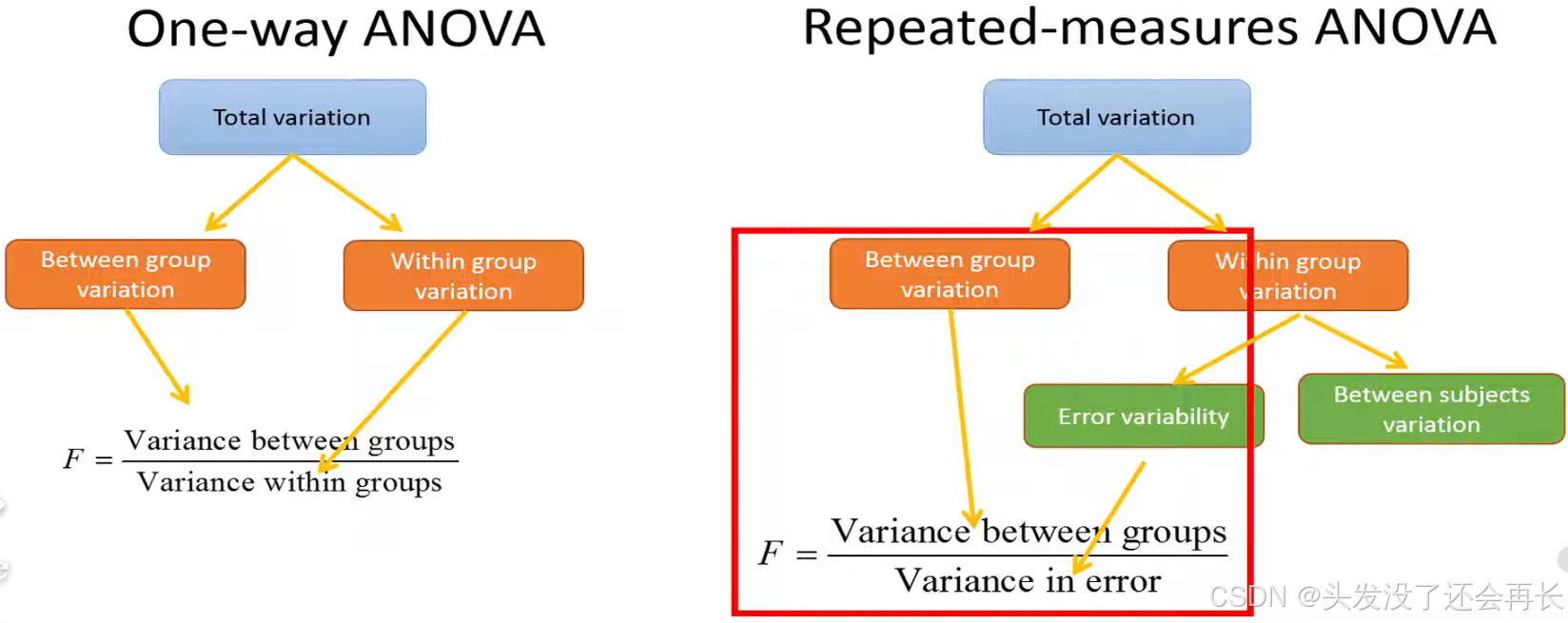
Example data
The weights, in kg, of four individuals have been measured before a certain diet, and then two and four weeks after starting the diet.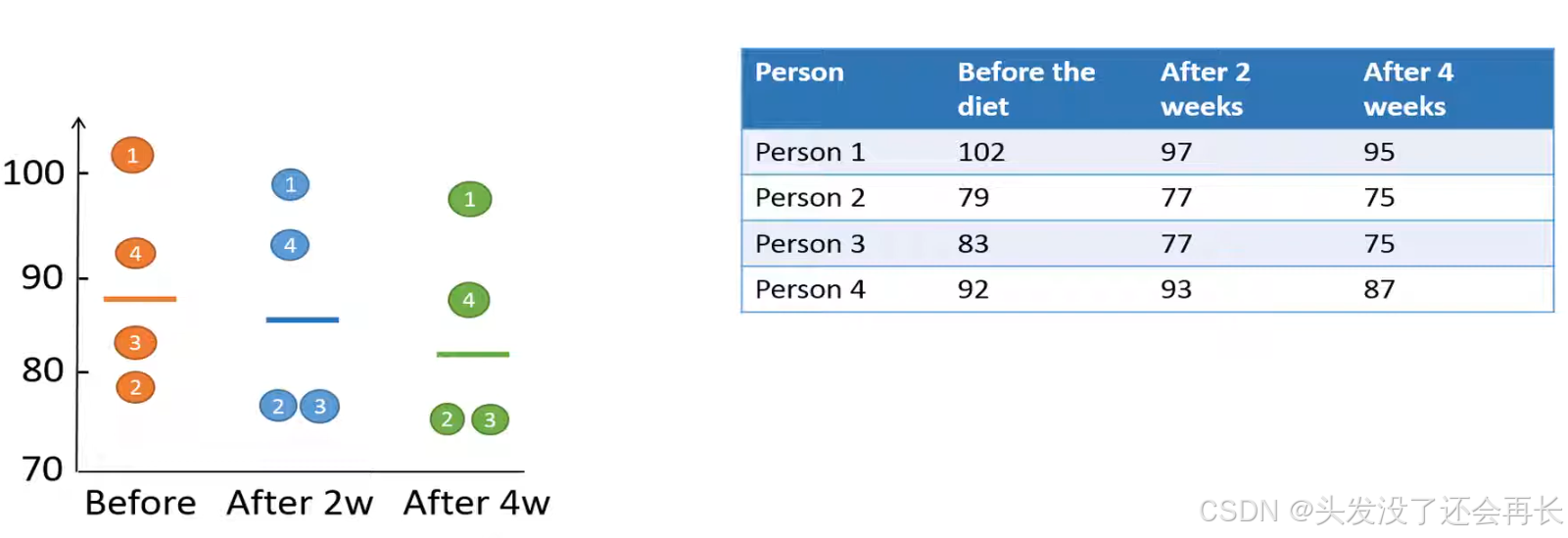
The null hypothesis is same as one-way ANOVA, the population mean weight is the same over the four weeks when people try this diet, we set the significance level is 0.05 in this example.
Repeated-measures ANOVA
The only difference from the one-way ANOVA is that the sum of squares within-groups is divided into between-subjects variation and an error term.
The error term is the variation that is left after we have removed the between-subjects variation from the within-group variation.
First, we can calculate variance within groups, SSW is calculated by following way: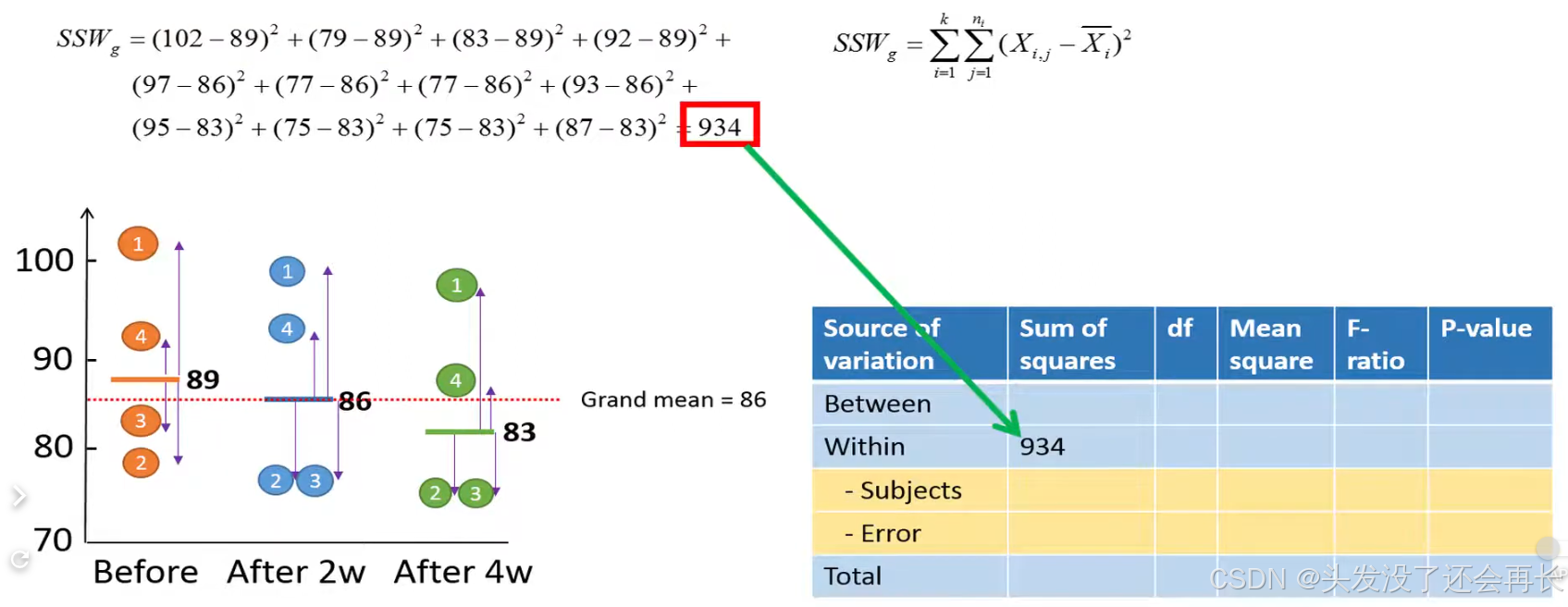
Note that the variation within the first group involves the variation in weights between the four individuals before diet. This variation has nothing to do with the effect of the diet. This is the reason why we will remove it in a later step.
Next, we calculate variance between groups, SSB is calculate by the following formula: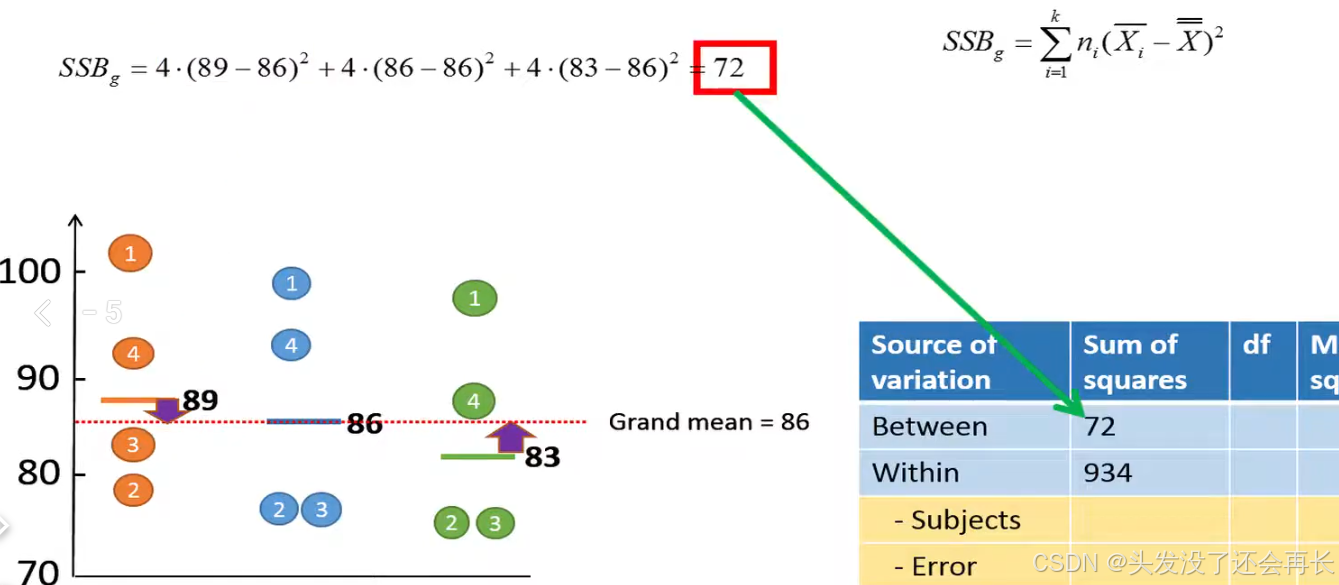
SST can also be calculated as the sum of SSB and SSW.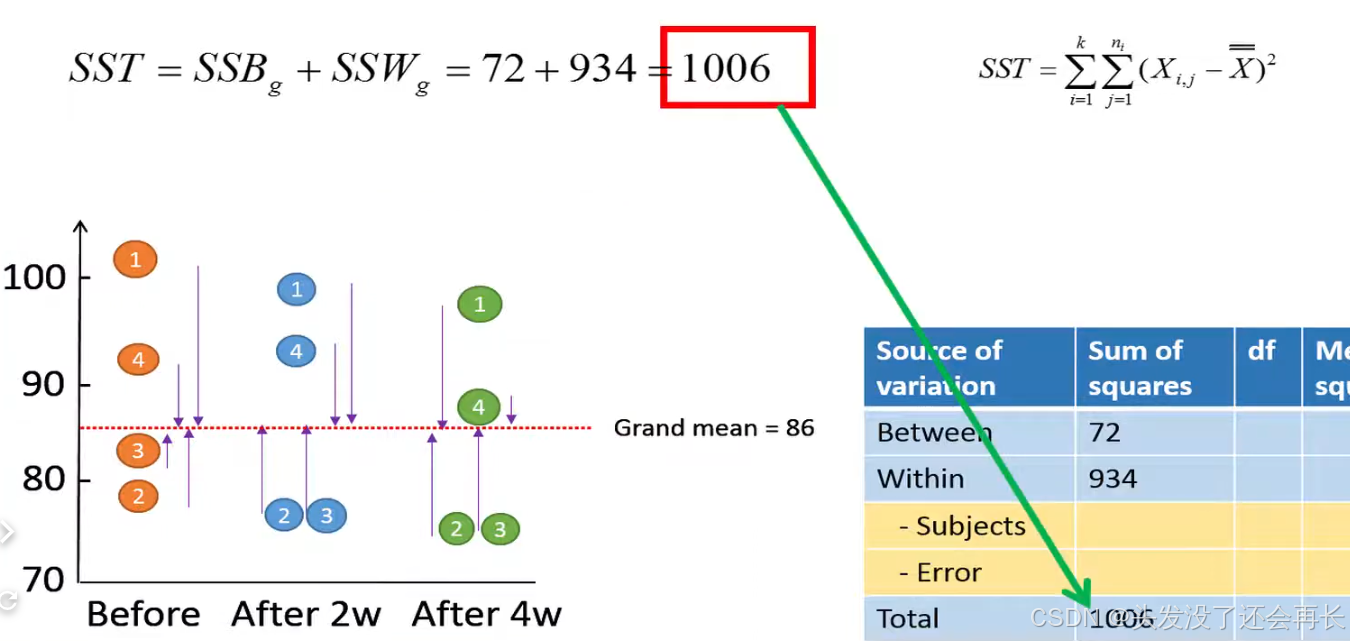
Then, we must calculate variance between subjects, the SSS is calculated by following formula: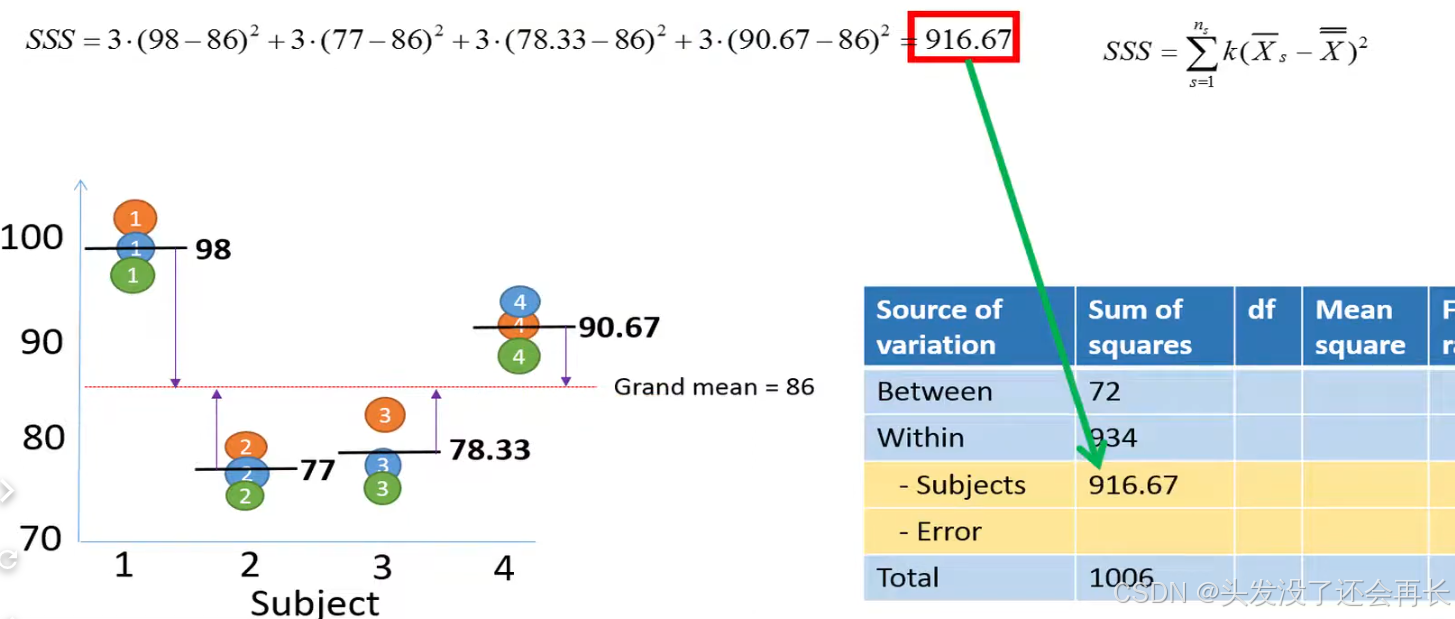
Then, we can calculate the term of error, which is simply the total within sum of squares minus the sum of squares for the subjects.
The degrees of freedom between-groups is the number of groups minus one;
The degrees of freedom within-groups is the total number of data points minus number of groups;
The degrees of freedom between subjects is the number of subjects minus 1;
The degrees of freedom for the error is the degrees of freedom of the total within-group variance minus the degrees of freedom for the subjects;
The degrees of freedom for the total sum of squares is the total number of data points minus one.
Next, we calculate the mean squares, which is simply the sum of squares divided by the corresponding degrees of freedom.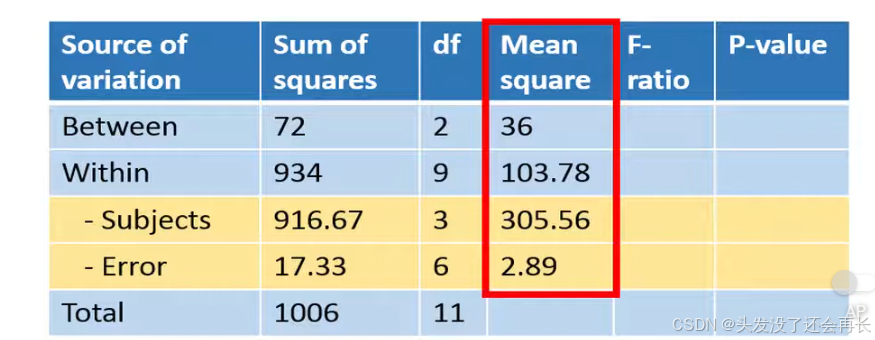
We can calculate F-ratio, which is the mean square of variance between groups divided by variance in error.
With the degree 2 and 6, we can get the area of t-distribution, which is our p value.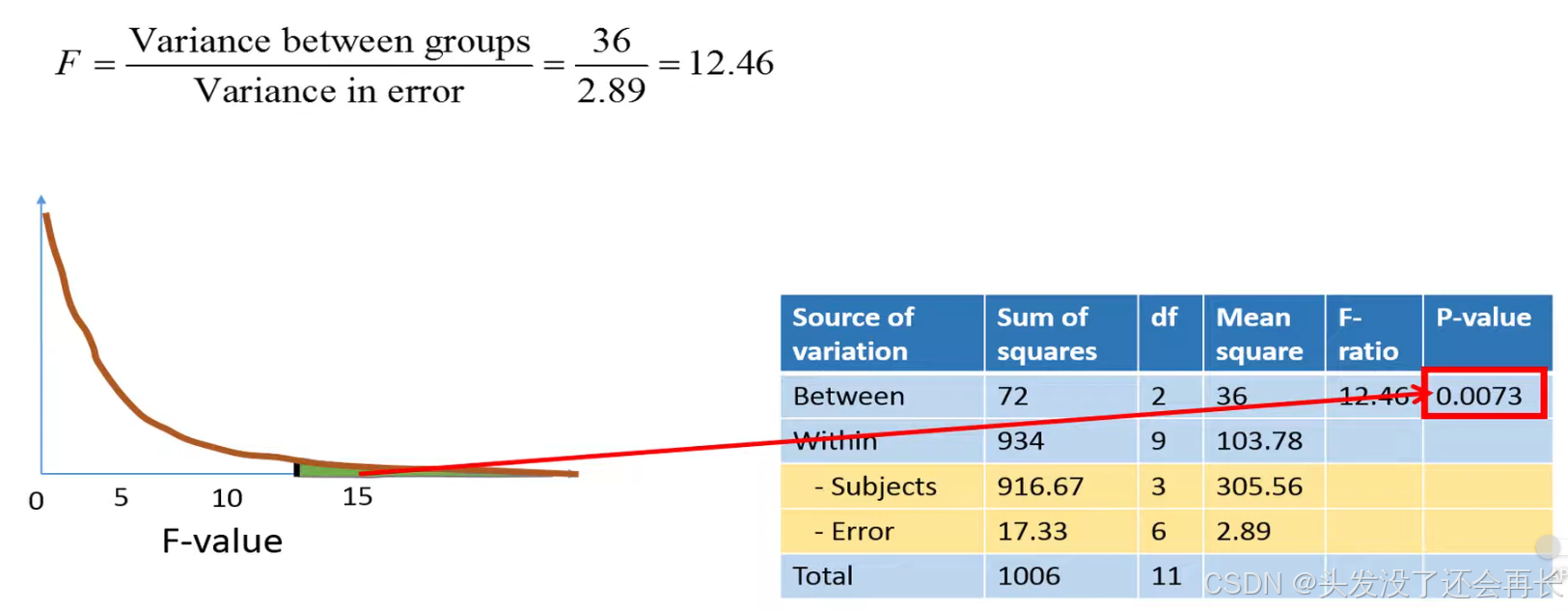
Because p value is below 0.05, so, we reject null hypothesis, we think at least two of the groups have a significance difference means.
To check which means that are different, we could run three separate paired t-tests. Only significant difference that can be observed is when we compare the first and third time-point.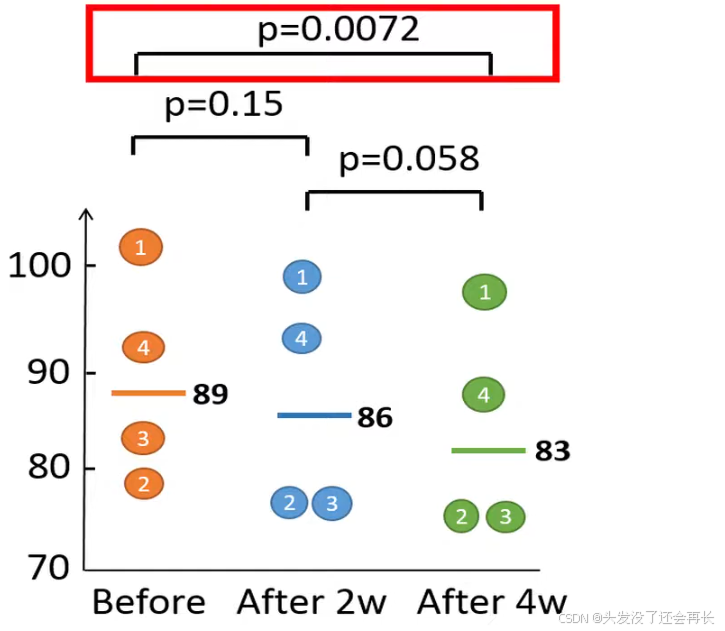
Results comparison between one-way / repeated ANOVA
The one-way ANOVA uses the total within variance in the denominator when calculating the F-ratio because it assumes that the groups contain observations of independent individuals, whereas the repeated-measures ANOVA removes the variance between the subjects because we are interested in how much each individual reduces in weight and not the variance in weights between the individuals.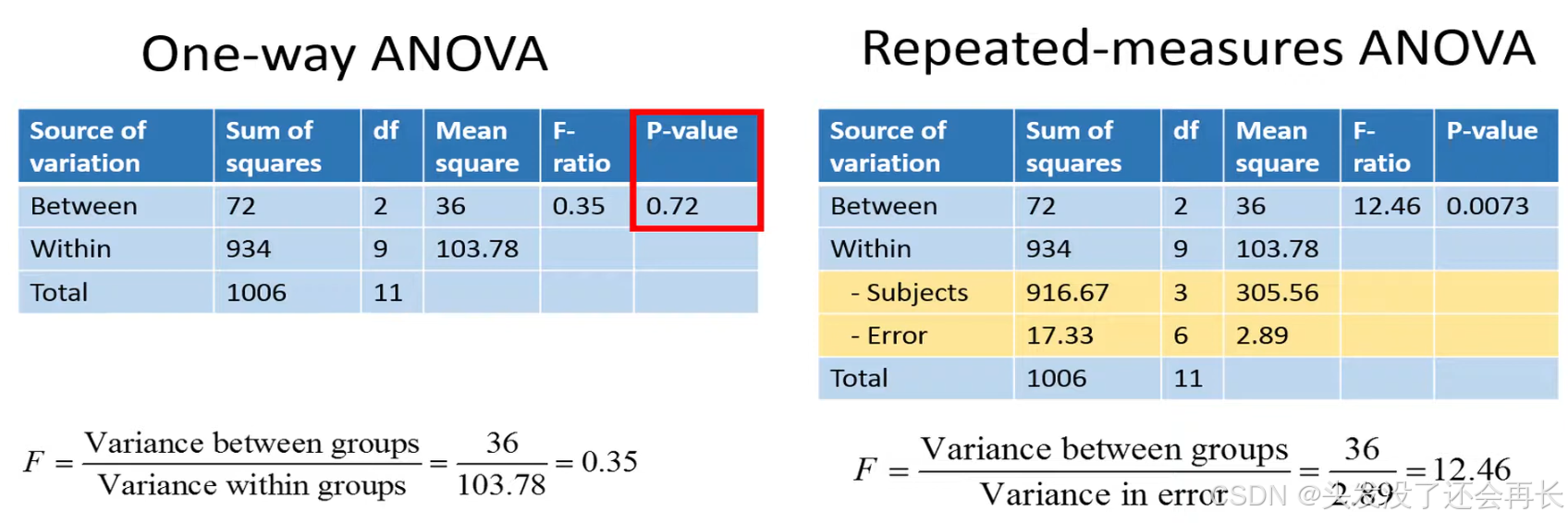
更多推荐
 已为社区贡献9条内容
已为社区贡献9条内容






所有评论(0)