（参考书：王高雄《常微分方程》第四版）

一、 存在唯一性定理的背景

01 皮卡逐步逼近序列

微分方程最大的问题就是难以求解，皮卡逐步逼近序列就是一种利用数值逼近的方法进行的求解。
我们知道微分方程指示了一个函数在不同点的导数和其自身的关系，那么对其导数进行积分近似便可以得到原函数。由莱布尼兹公式可以得到：
$$y-y_0={\int }_{x_0}^{x}f(x,y)dx$$
我们想求出$y$，设原函数$y$为$\phi (x)$，移项可得：
$$\phi (x)=\phi (x_0)+{\int }_{x_0}^{x}f(x,y)dx\text{\hspace{1em}(1)}$$
我们希望最理想的情况就是，这个式子是个显式，然后我们就可以直接求出$\phi (x)$，可惜观察发现，式子左右都含有$\phi (x)$，是个隐式。反正我们现在不需要求出精确解来，那么我们就采用一个数值逼近的方法，我们用$y_0$代替$y$（实际上$y$是个变量，我们现在把它近似成常数），用$(1)$式可以求出一个${\phi }_1(x)$，如此以来不断迭代，不断更新常数，不断趋近真正的$y$，我们可以获得一个皮卡逐步逼近序列：
$$\begin{gathered} {\phi }_1(x)=\phi (x_0)+{\int }_{x_0}^{x}f(x,{\phi }_0(x))dx \\ {\phi }_2(x)=\phi (x_0)+{\int }_{x_0}^{x}f(x,{\phi }_1(x))dx \\ \cdots \\ {\phi }_n(x)=\phi (x_0)+{\int }_{x_0}^{x}f(x,{\phi }_{n-1}(x))dx \end{gathered}$$
也就是
$$\{\begin{array}{l}{\phi }_0(x)=y_0\\ {\phi }_k(x)=\phi (x_0)+{\int }_{x_0}^{x}f(x,{\phi }_{k-1}(x))dx\end{array}$$
如果在迭代的过程中出现前后两个$\phi (x)$是相同的情况，那么它就是微分方程的解；如果一直都没有这种情况出现，那么这个序列最后会有一个极限值$\underset{n\to \infty }{\lim }{\phi }_n(x)=\phi (x)$，这个极限函数就是方程的解。

我们可以认为微分方程实际上是一个平面$f(x,y)$上满足$\frac{dy}{dx}=f(x,y)$的点连起来得到的线，可以看到，皮卡序列在初始处近似的时候，取$y=y_0$并使$f(x,y_0)$对$x$进行积分，得到效果如下所示，可以看到这个积分和我们想要的积分还是有差距的，但这毕竟只是近似，随着皮卡逐步逼近序列的迭代，我们的积分值会越来越接近真实的积分值。也就是说，我们在不断对积分值进行优化。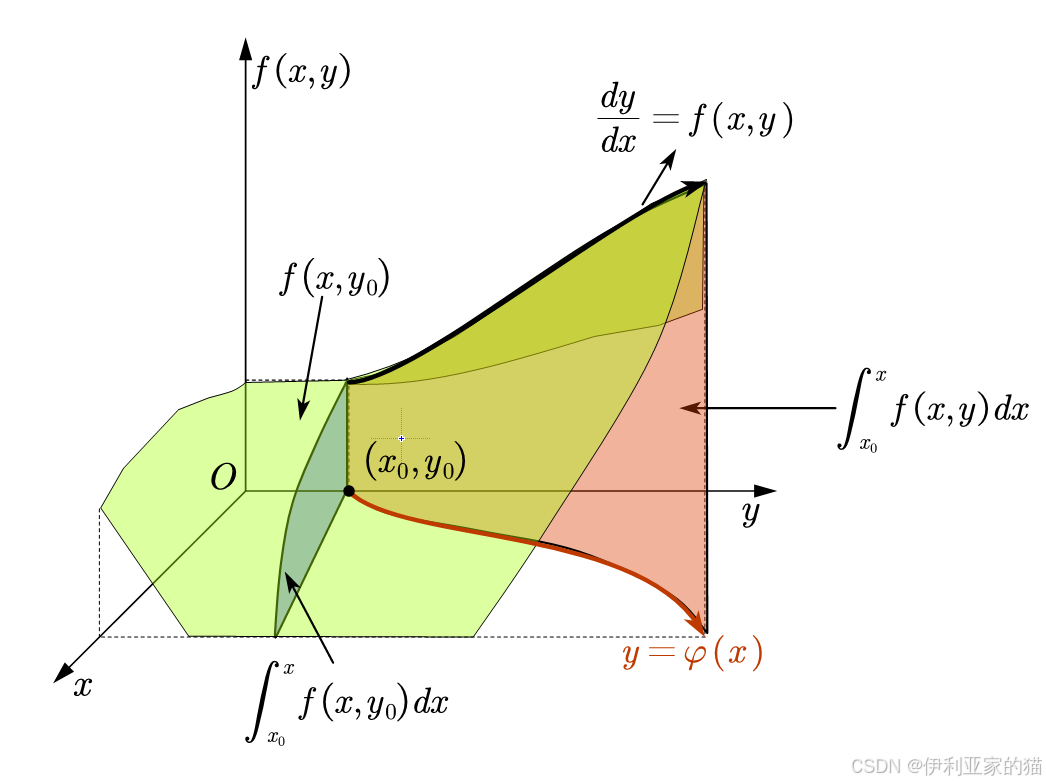

二、存在唯一性定理

01 利普西茨（Lipschitz）条件

对于一阶微分方程
$$\frac{dy}{dx}=f(x,y)$$
若$f(x,y)$满足对所有$(x,y_1),(x,y_2)\in R$都成立如下等式：
$$|f(x,y_1)-f(x,y_2)|\le \underset{利普西茨常数}{\underbrace{L}}|y_1-y_2|$$
则称$f(x,y)$满足利普西茨条件.

02 存在唯一性定理

除了皮卡逐步逼近序列之外，我们还关心一个问题，就是我们用皮卡序列得到了解之后？万一它本身是不存在的，或者解是不唯一的，那我们的皮卡序列就算求出一个解，也没办法找到另外的解，这样没有意义。这个时候寻找解的存在和唯一性显得尤为重要。

• 存在唯一性定理：
  若$f(x,y)$是在矩形区域$R:|x-x_0|\le a，|y-y_0|\le b$上的连续函数，且满足利普西茨条件，则在$|x-x_0|\le h$上存在唯一的解$y=\phi (x)$并满足初值条件$\phi (x_0)=y_0$.其中$h=\min \left(a,\frac{b}{M}\right)，M=\underset{(x,y)\in R}{\max }|f(x,y)|$

简单的推导就是假设$x$有一个限值$h$：
$$M|x-x_0|\le hM\le b$$
首先声明一点，满足利普西茨条件且在该矩形区域内连续的函数是肯定存在唯一解的，但是存在唯一解的函数一定满足利普西茨条件吗？未必。其实不止利普西茨条件，还有很多其他的条件都可以导出一阶微分方程解的存在唯一性，利普西茨条件只不过是解存在唯一的充分条件而已。那为什么课本上要写利普西茨条件呢？很简单，以为利普西茨条件比其他条件简洁好用。
再者，我们探讨一下利普西茨条件到底在讲什么，实际上就是由于我们手上有一个微分方程，且限定了$y$的范围，那么根据微分方程的关系，这个$y$范围一定能通过这个微分方程关系推出一个$x$的范围，再加上$x$本身在$a$为半径的邻域内，就得到了$|x-x_0|\le h=\min \left(a,\frac{b}{M}\right)$。
我们最理想的情况是，在全定义域范围内存在唯一解（这就相当于把整个微分方程解出来了），但事实上是做不到的，那么我们是否可以退而求其次，不要奢求全范围内的存在唯一性了，能在一个小范围内有存在唯一性就足够了，也就是牺牲一部分范围来获得存在唯一性。

• 利普西茨条件的本质是，我们可以通过微分方程关系，缩小存在唯一解的范围。

如下图所示，当$h<a$时，存在唯一解的范围就会被缩小到一个更小的区域$|x-x_0|\le h,|y-y_0|\le b$

三、近似计算和误差估计

在前面我们推导出了皮卡逐步逼近序列。前面我们分析过皮卡序列两种情况，一种是可以在有限步内前后两步的$\phi (x)$相等，此时便可以求出方程的解；另一种情况就是运气比较差，皮卡序列无限迭代都无法终止，此时只能取极限。
当然，计算机运行无限步骤的程序会卡死的，这个时候我们不能让他无限运行下去，我们知道越往后的皮卡序列肯定越接近真正的解，但是我们等不到那个时候了，我们得让它在有限步内终止。那么我们取第$k$步的近似解${\phi }_k(x)$就足够了。
这个时候我们最关心的是，近似解${\phi }_k$的误差是多少？如果误差在可以忍受的范围内，那我们就接受这个解。我们有误差估计式：
$$|{\phi }_k(x)-\phi (x)|\le \frac{M{L}^k}{(k+1)!}{h}^{k+1}$$

• 其中各个量的含义为：
  { M = max ⁡ ∣ f ( x , y ) ∣ L = max ⁡ ∂ f ∂ y ( 由于利普西茨条件在实际中难以满足，通常采用该式为充分条件进行计算 ) h = min ⁡ { a , b M } k : 迭代次数 \begin{cases} M=\max |f(x,y)| \\ L=\max \frac{\partial f}{\partial y}\quad(由于利普西茨条件在实际中难以满足，通常采用该式为充分条件进行计算)\\ h=\min \{ a,\frac b M\}\\ k:迭代次数 \end{cases} ⎩ ⎨ ⎧​M=max∣f(x,y)∣L=max∂y∂f​(由于利普西茨条件在实际中难以满足，通常采用该式为充分条件进行计算)h=min{a,Mb​}k:迭代次数​

我们以自己可以忍受的误差作为标准取一个合适的解${\phi }_k$。

四、总结

从上面可以看出，实际上一阶微分方程解的存在唯一性定理这一章是一个连贯的过程。
$$微分方程难以求解\to \underset{\begin{array}{c}\\ \downarrow \\ \\ 皮卡逐步逼近序列\end{array}}{\mathrm{获取数值解}}\to \underset{\begin{array}{c}\\ \downarrow \\ \\ 存在唯一性定理\end{array}}{\mathrm{保证求出的解是唯一的}}\to \underset{\begin{array}{c}\\ \downarrow \\ \\ 近似计算与误差估计\end{array}}{\mathrm{解是否有效}}$$