非线性方程的迭代解法及其收敛性
在解非线性方程时,如代数方程(二次、三次等),超越方程(三角方程,指数、对数方程等),即使是基本的代数方程,当次数超过4时,就不能用公式法表示方程的根了。因此需要使用数值方法计算非线性方程的根。...
引言
在科学计算中会遇到大量求解非线性方程的情况。如代数方程(二次、三次等),超越方程(三角方程,指数、对数方程等)。即便是基本的代数方程,当次数超过4次时,一般就不能用公式表示方程的根了。为了解决这些问题就要用到数值方法了。
简单迭代法
先将f(x)=0f(x)=0f(x)=0化为一个与它同解的方程x=φ(x)x=\varphi(x)x=φ(x),即如果数α\alphaα使得f(α)=0f(\alpha)=0f(α)=0,则有α=φ(α)\alpha=\varphi(\alpha)α=φ(α),反之亦然。这样我们就可以构造一个迭代过程,来求出α\alphaα的近似值。
任取初始值x0x_0x0,得x1=φ(x0)x_1=\varphi(x_0)x1=φ(x0),再把x1x_1x1带入,求得x2=φ(x1)x_2=\varphi(x_1)x2=φ(x1),继为之,便可得到一个数列。一般表示形式为xk+1=φ(xk)(k=0,1,2,...)x_{k+1}=\varphi(x_k)(k=0,1,2,...)xk+1=φ(xk)(k=0,1,2,...)。这就是求解非线性方程的简单迭代法(迭代法、迭代过程、迭代格式),φ(x)\varphi(x)φ(x)为迭代函数,xkx_kxk称第k步的迭代值。
如果由迭代格式产生的数列收敛,即limk→∞xk=α\lim\limits_{k\to\infty}x_k=\alphak→∞limxk=α,则称迭代法收敛,否则称迭代法发散。若收敛,α\alphaα就是方程的根
来看个例子:求f(x)=2x3−x−1f(x)=2x^3-x-1f(x)=2x3−x−1的根。用迭代法,我们化为等价方程x=x+123x=\sqrt[3]{\frac{x+1}{2}}x=32x+1,则迭代公式为xk+1=xk+123x_{k+1}=\sqrt[3]{\frac{x_k+1}{2}}xk+1=32xk+1。或者化为x=2x3−1x=2x^3-1x=2x3−1,迭代格式:xk+1=2xk3−1x_{k+1}=2x_k^3-1xk+1=2xk3−1,初始值都取x0=0x_0=0x0=0,计算后发现一个收敛一个发散。这说明,迭代法的收敛与发散,依赖于迭代函数
迭代函数构造的方法很多,例如x−f(x)=xx-f(x)=xx−f(x)=x,进一步x−k(x)f(x)=x,(k(x)≠0)x-k(x)f(x)=x,(k(x)\neq0)x−k(x)f(x)=x,(k(x)=0)。那么迭代函数要满足什么条件,迭代法才收敛呢?从下图可以看出:
迭代函数满足φ′(x)<1\varphi^{'}(x)<1φ′(x)<1时,迭代法收敛。
迭代终止条件与迭代次数
来看一个定理:设迭代函数φ(x)\varphi(x)φ(x)满足,1、当x∈[a,b]时,a≤φ(x)≤bx\in[a,b]时,a\leq\varphi(x)\leq bx∈[a,b]时,a≤φ(x)≤b。2、存在正数0<L<10<L<10<L<1,对任意x∈[a,b]均有∣φ′(x)∣≤Lx\in[a,b]均有|\varphi^{'}(x)|\leq Lx∈[a,b]均有∣φ′(x)∣≤L,则x=φ(x)x=\varphi(x)x=φ(x)在[a,b]内存在唯一根α\alphaα,且对任意初始值x0∈[a,b]x_0\in[a,b]x0∈[a,b],迭代法收敛于α\alphaα,且有:1式∣xk−α∣≤L1−L∣xk−xk−1∣|x_k-\alpha|\leq \frac{L}{1-L}|x_k-x_{k-1}|∣xk−α∣≤1−LL∣xk−xk−1∣以及2式∣xk−α∣≤Lk1−L∣x1−x0∣|x_k-\alpha|\leq \frac{L^k}{1-L}|x_1-x_{0}|∣xk−α∣≤1−LLk∣x1−x0∣
从这个定理来看,相邻两次计算值的偏差∣xk−xk−1∣|x_k-x_{k-1}|∣xk−xk−1∣达到事先给定的精度要求,迭代过程就可以终止。由2式可以大概估计迭代过程所需要的迭代次数。但是由于定理的条件一般很难验证,也不一定成立。所以在根附近进行迭代。由2式可以看出,当L或∣φ′(x)∣|\varphi^{'}(x)|∣φ′(x)∣在[a,b]上的值越小,迭代过程收敛速度就越快,当L<1且接近1时,收敛速度很慢。
收敛速度的阶
为了使收敛速度有定量的判断,引入收敛速度的阶概念。设迭代格式xk+1=φ(xk)x_{k+1}=\varphi(x_k)xk+1=φ(xk),当k→∞k\to\inftyk→∞时,xk+1→αx_{k+1}\to\alphaxk+1→α,并记ek=xk−αe_{k}=x_k-\alphaek=xk−α。
若存在实数p≥1,c>0满足limk→∞∣ek+1∣∣ek∣p=cp\geq1,c>0满足\lim\limits_{k\to\infty}\frac{|e_{k+1}|}{|e_k|^p}=cp≥1,c>0满足k→∞lim∣ek∣p∣ek+1∣=c,则称迭代法是p阶收敛。
当p=1时,称为线性收敛;
当p>1时,称为超线性收敛;
当p=2时,称为平方收敛;
p越大迭代法收敛速度越快。
那p如何确定呢,有定理:
如果x=φ(x)x=\varphi(x)x=φ(x)中的迭代函数在根α\alphaα附近满足:
(1)φ(x)\varphi(x)φ(x)存在p阶连续导函数
(2)φ′(α)=φ′′(α)=...=φp−1(α)=0,φp(α)≠0\varphi^{'}(\alpha)=\varphi^{''}(\alpha)=...=\varphi^{p-1}(\alpha)=0,\varphi^{p}(\alpha)\neq0φ′(α)=φ′′(α)=...=φp−1(α)=0,φp(α)=0则迭代法xk+1=φ(xk)x_{k+1}=\varphi(x_k)xk+1=φ(xk)是p阶收敛。
Newton迭代法及其变形
用迭代法求解非线性方程,构造迭代函数使其收敛非常重要。无论非线性方程f(x)=0形式如何,总有以下构造方法:
x=φ(x)=x−k(x)f(x),(k(x)≠0)x=\varphi(x)=x-k(x)f(x),(k(x)\neq0)x=φ(x)=x−k(x)f(x),(k(x)=0)
前面说过迭代函数的导数绝对值小于1则收敛,且越小收敛速度越快,我们令其导函数为0。有以下推算:
由此引出定理:
方程f(x)=0的根为α,f′(α)≠0\alpha,f^{'}(\alpha)\neq0α,f′(α)=0则:
式4-26带有f(x)的导函数,使用不方便,用其近似值代替,有:
我们来看下它们的几何意义:


从图中也可看出,弦截法需要两个初值。
Newton法的收敛性与初始值的选取有很大关系(在根附近讨论,局部收敛性)。初始值选择不当,会导致发散,下面介绍一种大范围内收敛的方法。
一种大范围收敛的Newton型方法
为了防止迭代发散,我们符加一个条件:
其中的下山因子一般采用试算法。由迭代得到xkx_kxk后,取不同的λ\lambdaλ进行试算,例如:1,1/2,1/4,1/8…。计算出xk+1x_{k+1}xk+1后接着计算f(xk+1)f(x_{k+1})f(xk+1),如果∣f(xk+1)∣<∣f(xk)∣|f(x_{k+1})|<|f(x_{k})|∣f(xk+1)∣<∣f(xk)∣成立,则xk+1x_{k+1}xk+1为第k+1步的迭代值。再取λ\lambdaλ按照上一步接着计算xk+2x_{k+2}xk+2,如果计算过程中遇到一个迭代值xkx_{k}xk取不到满足要求的λ\lambdaλ值,则称“下山失败”。这时需要另取初始值x0x_{0}x0进行重新计算。
多根区间上的逐次逼近法
方程f(x)=0在多根区间[a,b]上,根的情况无非两种。均为单根或有重根。我们先看均为单根的情况:
1)首先求出单根区间,假设有m个根。把[a,b]分成n个小区间。[b0,b1],[b1,b2],...[bn−1,bn],(b0=a,bn=b)[b_0,b_1],[b_1,b_2],...[b_{n-1},b_n],(b_0=a,b_n=b)[b0,b1],[b1,b2],...[bn−1,bn],(b0=a,bn=b)然后计算f(bi)(i=1,2,...,n)f(b_i)(i=1,2,...,n)f(bi)(i=1,2,...,n)的值,当f(bi)f(bi+1)<0f(b_i)f(b_{i+1})<0f(bi)f(bi+1)<0时,那在[bi,bi+1][b_i,b_{i+1}][bi,bi+1]上至少有一个根。如果有m个区间是这样,那所得到的就都是单根区间。如果这样的有根区间小于m,那就把这些区间再对分,然后重复上述计算直到有m个有根区间为止。
2)再在单根区间上求解。这个就回到之前讲的了。这里介绍一种搜索法。可用来求迭代法的初始值,也可求近似根:

如果发现用二分法过程中,趋于零的速度慢,可以从某个区间开始用迭代法,用该区间端点作为初始值。
再看有重根的情况:
通过计算得出:在重根条件下的Newton 迭代法如果收敛, 必是线性收敛的。为了提高收敛的阶,可取:
这样迭代函数至少是平方收敛。可以看个例子: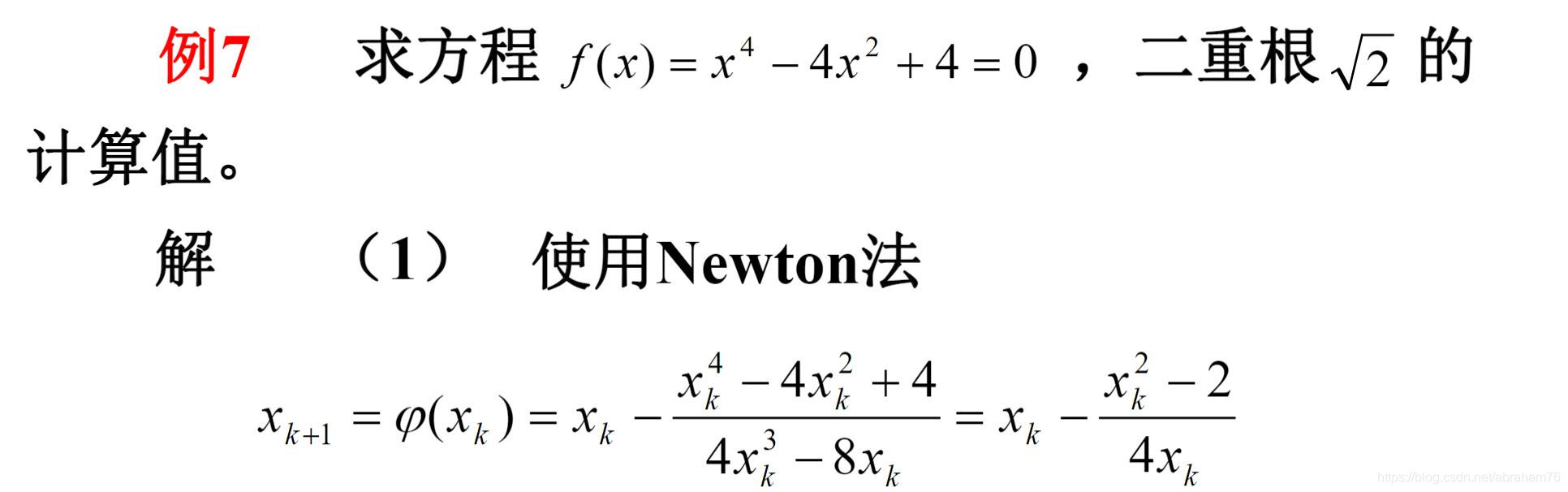

更多推荐
 已为社区贡献9条内容
已为社区贡献9条内容







所有评论(0)