使用最小最大插值的非均匀快速傅里叶变换

J. A. Fessler and B. P. Sutton, “Nonuniform fast Fourier transforms using min-max interpolation,” in IEEE Transactions on Signal Processing, vol. 51, no. 2, pp. 560-574, Feb. 2003, doi: 10.1109/TSP.2002.807005.

引言与背景

快速傅里叶变换（FFT）在信号处理领域中被广泛应用，它能够高效地计算有限长度信号在均匀间隔频率位置上的傅里叶变换。对于N点信号，FFT只需要O(N log N)次运算，而直接计算离散傅里叶变换则需要O(N²)次运算。然而，在许多应用中，我们需要在频域进行非均匀采样，这就是非均匀傅里叶变换（Nonuniform Fourier Transform）的需求所在。

这类应用已经被认识了至少30年，包括雷达成像、通过Radon变换计算定向小波、计算电磁学、FIR滤波器设计等。本文作者的工作特别受到迭代磁共振图像（MRI）重建和基于傅里叶切片定理的迭代断层图像重建方法的启发。这些问题与从非均匀样本重建带限信号的问题密切相关。

一维理论推导

问题的数学表述

给定均匀间隔的信号样本 $x_n$，其中 $n=0,\dots ,N-1$，对应的傅里叶变换为：

$$X(\omega )=\sum _{n=0}^{N-1}{x}_n{e}^{-i\omega n}$$

我们希望在一组（非均匀间隔的）频率位置 ${\omega }_m$ 处计算傅里叶变换：

$${\hat{X}}_m\triangleq X({\omega }_m)=\sum _{n=0}^{N-1}{x}_n{e}^{-i{\omega }_{m}n},m=1,\dots ,M$$

这里的符号"$\triangleq$"表示"定义为"。频率位置 ${\omega }_m$ 可以是任意实数。这种形式被称为非均匀离散傅里叶变换（NDFT）。直接计算上式需要O(MN)次运算，对于大规模问题来说计算量过大。快速计算这个表达式就是NUFFT的目标。

NUFFT方法的两步框架

大多数NUFFT方法的第一步是选择一个合适的过采样因子K ≥ 1，并计算加权的K·N点FFT：

$$Y_k=\sum _{n=0}^{N-1}{s}_n{x}_n{e}^{-i\gamma kn},k=0,\dots ,K\cdot N-1$$

其中 $\gamma \triangleq 2\pi /K$ 是K·N点DFT的基频。非零的 $s_n$ 是算法设计变量，被称为"缩放因子"。我们将 $\mathbf{s}=(s_1,\dots ,s_N)$ 称为缩放向量。$\mathbf{s}$ 的目的是部分预补偿后续频域插值中的不完美性。

第二步是通过插值 $Y_k$ 来近似每个 ${\hat{X}}_m$，使用 ${\omega }_m$ 在DFT频率集 ΩK≜{0,γ,2γ,…,(K⋅N−1)γ}\Omega_K \triangleq \{0, \gamma, 2\gamma, \ldots, (K \cdot N - 1)\gamma\}ΩK​≜{0,γ,2γ,…,(K⋅N−1)γ} 中的某些邻居。线性插值器的一般形式为：

$$\hat{X}({\omega }_m)=\sum _{k=0}^{K-1}{v}_{m,k}^{\ast }{Y}_k=⟨\mathbf{Y},{\mathbf{v}}_m⟩,m=1,\dots ,M$$

最小最大插值器的推导

本文采用最小最大准则来选择插值系数 {uj(ωm)}\{u_j(\omega_m)\}{uj​(ωm​)}。对于每个期望的频率位置 ${\omega }_m$，我们确定系数向量 $\mathbf{u}({\omega }_m)\in {\mathbb{C}}^J$，使其最小化 ${\hat{X}}_m$ 和 $X_m$ 之间在所有单位范数信号上的最坏情况近似误差：

$$\mathbf{u}({\omega }_m)=\arg \underset{\mathbf{u}\in {\mathbb{C}}^J}{\min }\underset{\Vert \mathbf{x}{\Vert }_2=1}{\max }|\hat{X}({\omega }_m)-X({\omega }_m)|$$

从数学上讲，这个最小最大问题变为：

$$\underset{\mathbf{u}({\omega }_m)\in {\mathbb{C}}^J}{\min }\underset{\mathbf{x}\in {\mathbb{C}}^N:\Vert \mathbf{x}{\Vert }_2\le 1}{\max }|\hat{X}({\omega }_m)-X({\omega }_m)|$$

值得注意的是，这个最小最大问题有解析解。通过Cauchy-Schwarz不等式，对于给定频率 $\omega$，最坏情况信号是 $\mathbf{x}={\mathbf{q}}^{\ast }(\omega )/\Vert \mathbf{q}(\omega )\Vert$，即：

$$\underset{\Vert \mathbf{x}\Vert =1}{\max }|⟨\mathbf{x},\mathbf{q}(\omega )⟩|=\Vert \mathbf{q}(\omega )\Vert$$

将此代入最小最大准则并应用相关公式，最小最大问题简化为以下最小二乘问题：

$$\underset{\mathbf{u}(\omega )}{\min }\Vert {\mathbf{S}}^{\ast }\mathbf{C}\Lambda (\omega )\mathbf{u}(\omega )-\mathbf{b}(\omega ){\Vert }^2$$

该普通最小二乘问题的最小值为 $\omega ={\omega }_m$，其中：

$$\mathbf{u}(\omega )={\mathbf{A}}^{†}(\omega )[{\mathbf{C}}^{\ast }\mathbf{S}{\mathbf{S}}^{\ast }\mathbf{C}{]}^{-1}{\mathbf{C}}^{\ast }\mathbf{Sb}(\omega )$$

由于 $\mathbf{S}$ 是酉矩阵，这就是最小最大插值器的一般表达式。

图形分析与可视化

图1：J=6, K/N=2时的最小最大插值器

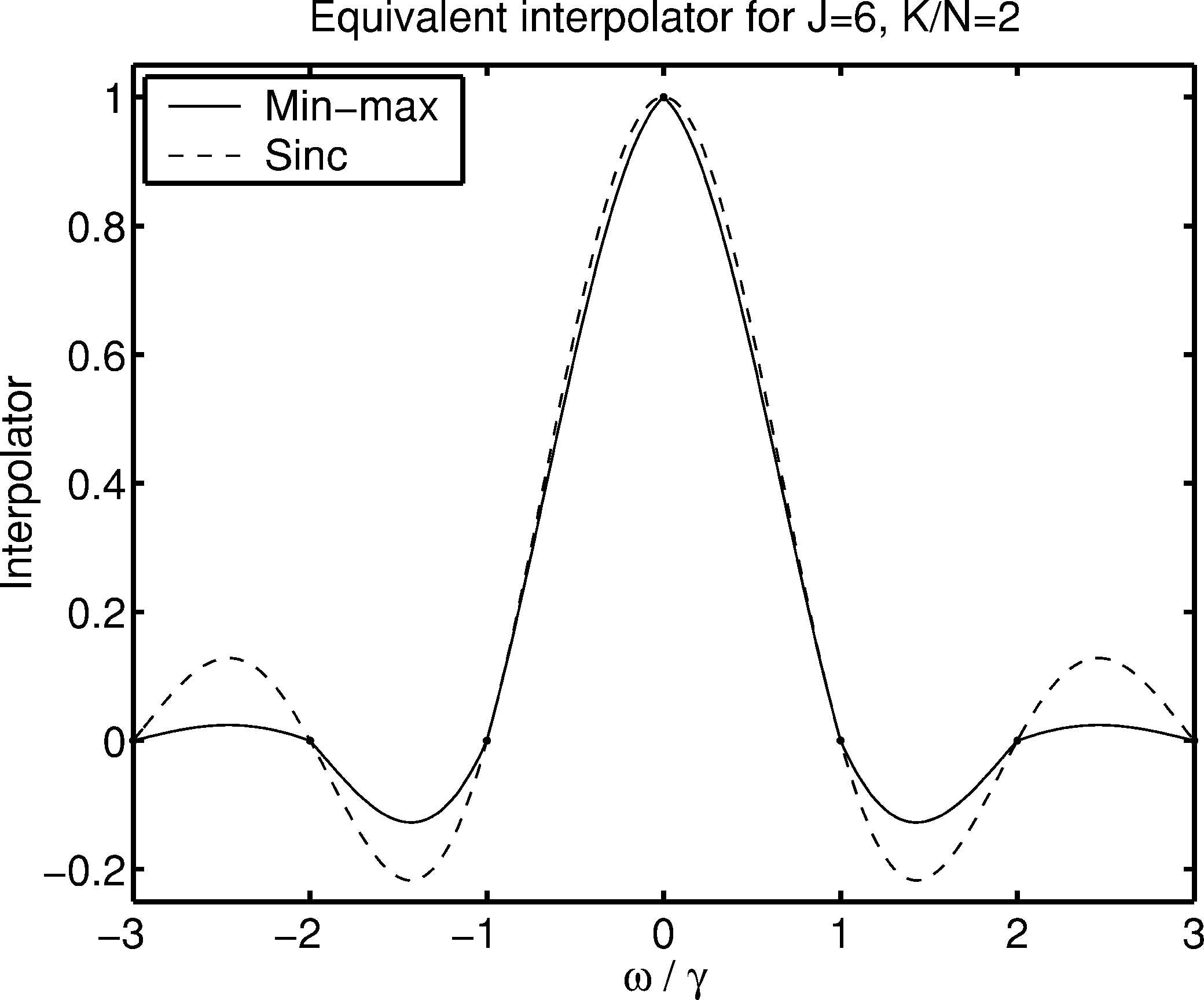
图1 展示了J=6、N=128、K/N=2和均匀缩放因子条件下对应于公式(33)的最小最大插值器。图中实线表示最小最大插值器，虚线表示sinc插值器的一部分。这个图揭示了几个重要特征：最小最大插值器在整数参数处不可微。插值器在零处的值并非恰好为1，在其他DFT样本点也不为零，这与经典插值器的性质有显著差异。尽管表面上看起来最小最大插值器与（截断的）理想Dirichlet插值器相似，但图1中看似微小的差异会强烈影响最大误差。

图2：J=7时的插值器比较

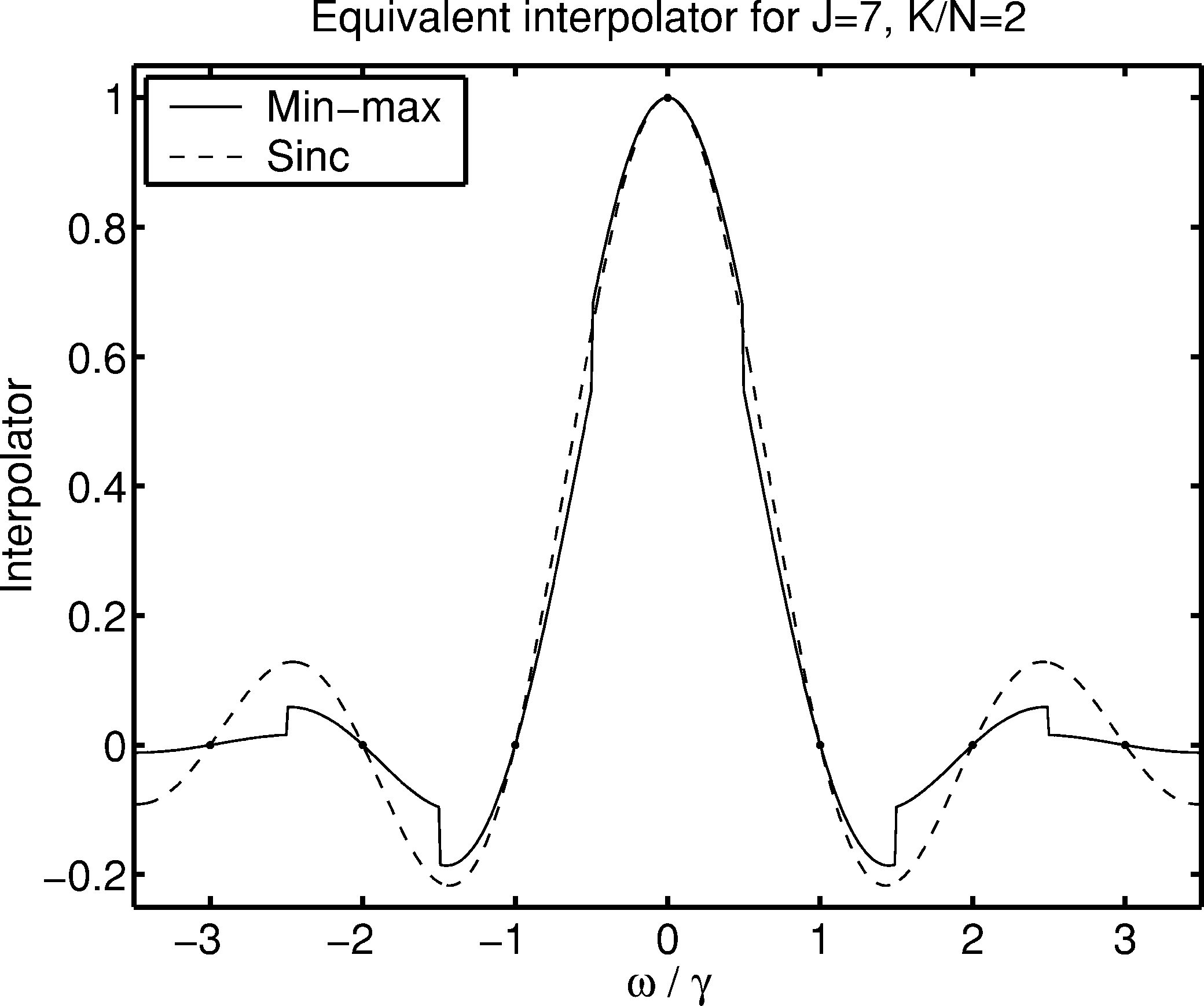
图2 展示了J=7、N=128、K/N=2和均匀缩放因子条件下的最小最大插值器。对于奇数J，最小最大插值器在DFT样本之间的中点处有不连续性，因为在该点邻域发生变化。这些特性与经典插值器有很大差异，但它们不必令人惊讶，因为规律性不是最小最大公式的一部分。

图3：不同J和K/N值的最大误差

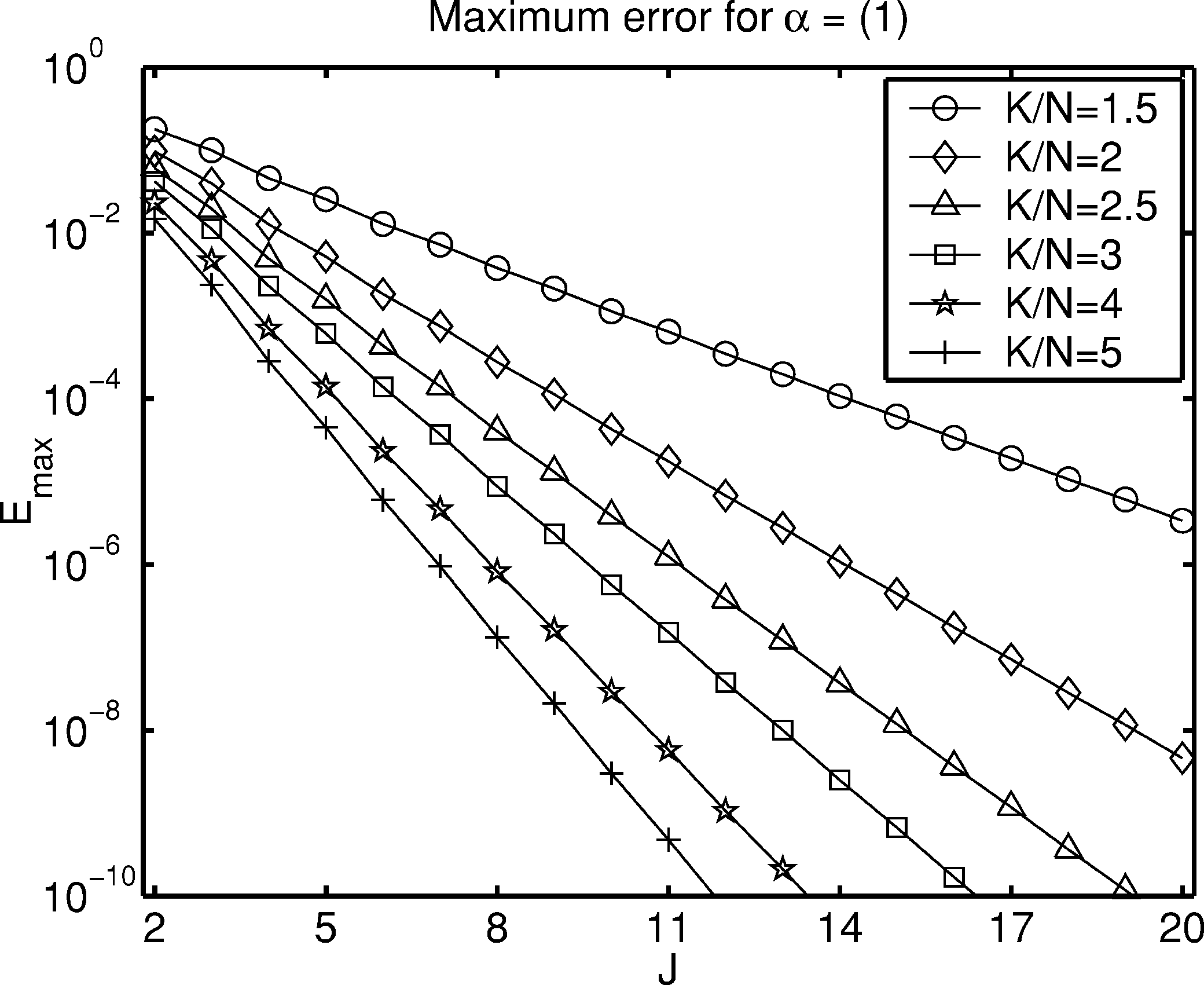
图3 绘制了使用均匀缩放向量（s=1）时，各种邻域大小J和过采样因子K/N的最小最大插值器的最大误差 ${\mathcal{E}}_{\max }$。图中显示了从K/N=1.5到K/N=5的多条曲线。如预期的那样，增加K或J会减少误差，但收益递减。通过检查许多这样的曲线，作者拟合了以下经验公式：

$${\mathcal{E}}_{\max }\approx 0.75\exp \left(-J\left[0.29+1.03\log \left(\frac{K}{N}\right)\right]\right)$$

图6：缩放向量优化的效果

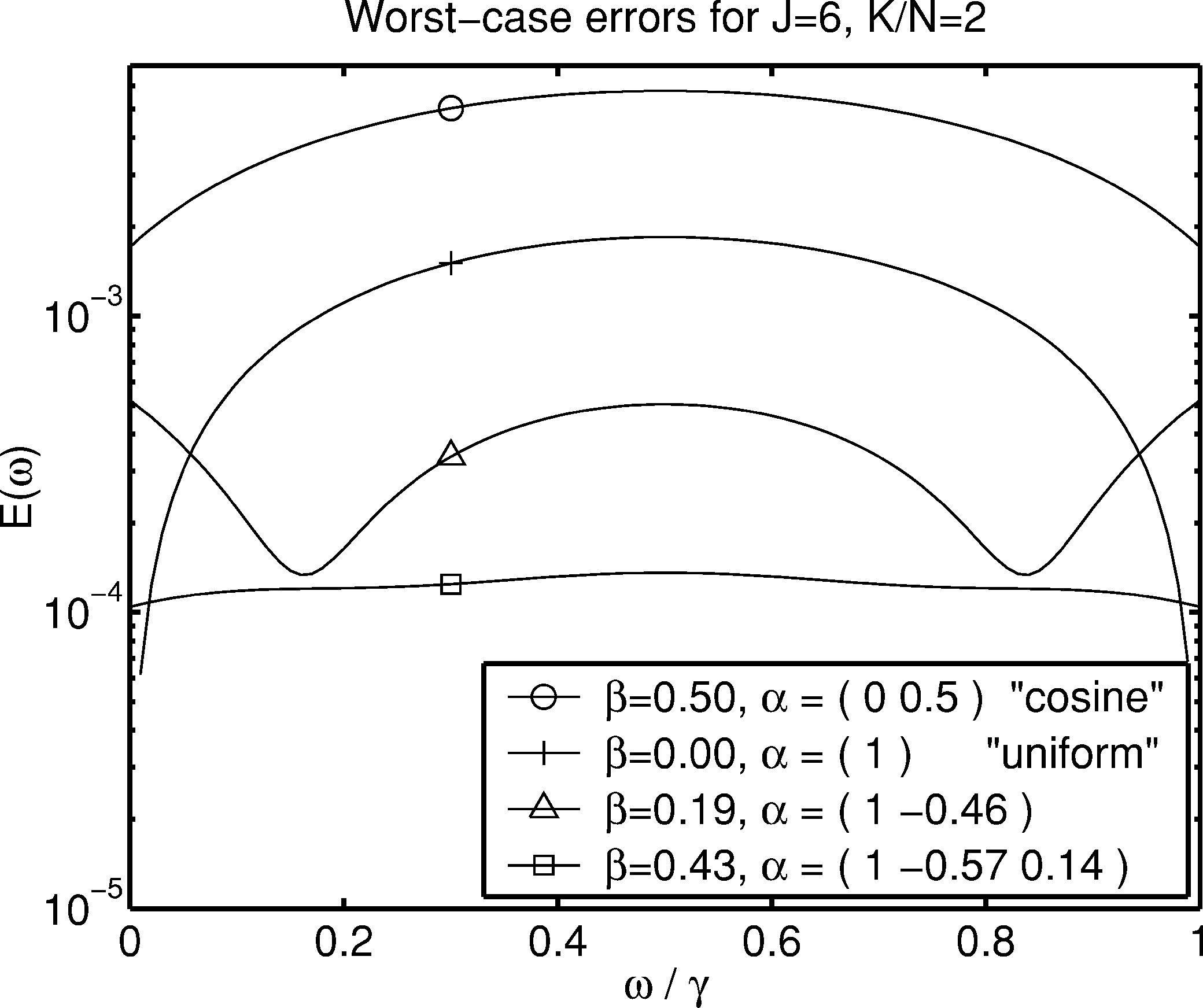
图6 比较了各种缩放向量的最坏情况误差。图中展示了三种情况：均匀缩放因子（$\beta =0.50,\alpha =(0,0.5)$），优化的缩放因子（$\beta =0.00,\alpha =(1)$），以及具有特定参数的情况。优化的缩放因子倾向于平衡DFT样本处和中点处的误差。实践中这种特性更可取，因为期望的频率位置通常具有本质上的随机位置。

与传统插值方法的详细比较

截断的Dirichlet插值器

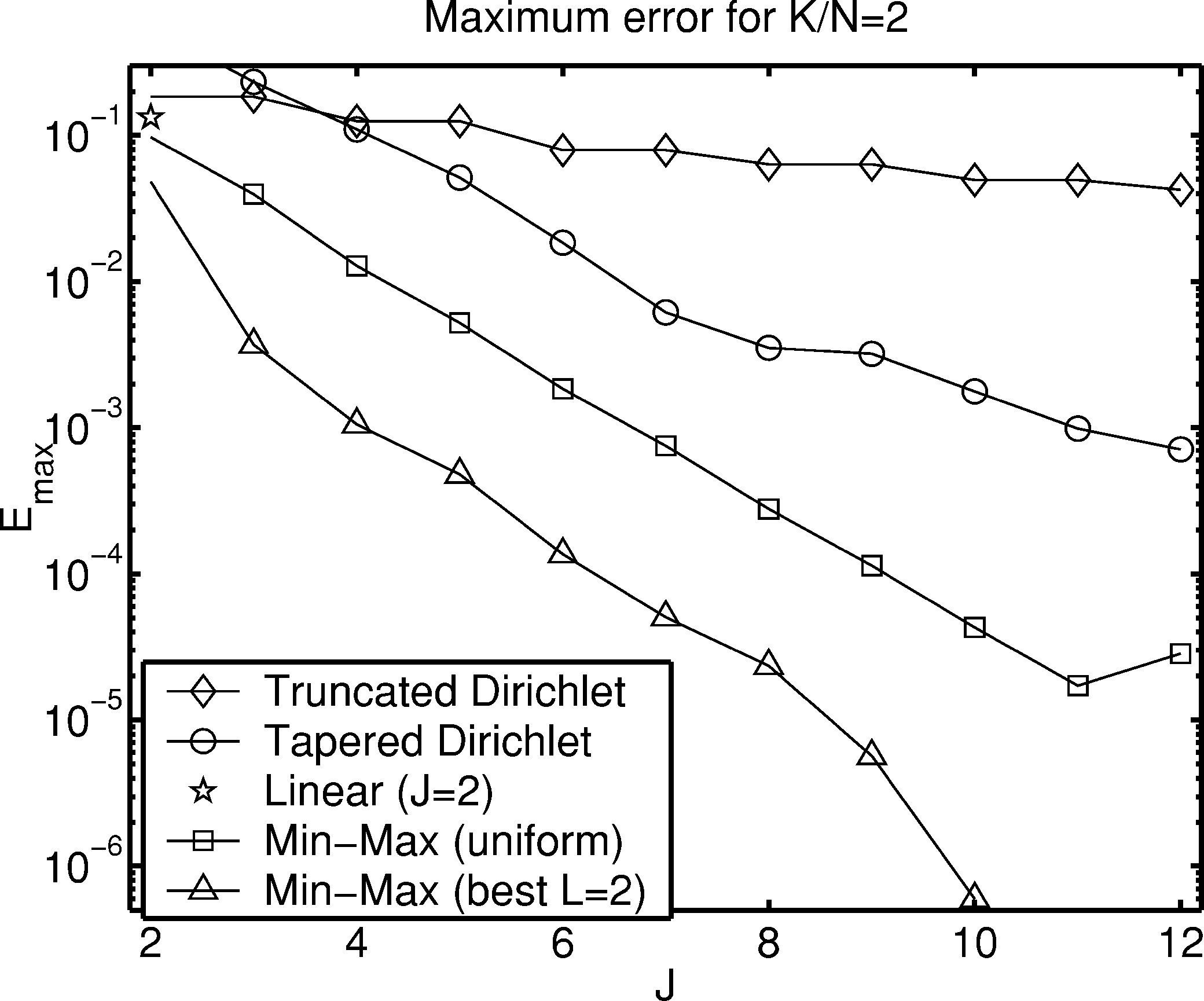
图8展示了截断Dirichlet插值器、${\cos }^2$锥形Dirichlet插值器、线性插值器（J=2）和最小最大插值器在各种邻域大小J和过采样因子K/N=2下的最大误差。尽管图1中存在相似性，但最小最大方法相对于截断或锥形Dirichlet显著减少了误差。对于J=6，最小最大插值器的误差比截断Dirichlet低约两个数量级。

高斯钟形插值器

许多NUFFT论文都关注使用截断高斯钟形插值的方法：

$$\psi (\kappa )=e^{-(\kappa /\sigma {)}^2/2}\text{rect}\left(\frac{\kappa }{\gamma J}\right)$$

图9比较了最小最大插值器和优化高斯钟形插值的最大误差。对于每个J，通过穷举搜索在数值上优化了高斯钟形宽度σ以最小化最坏情况误差。图中显示了最小最大方法的三种缩放因子选择：均匀、数值优化和对优化高斯钟形的LS拟合。

Kaiser-Bessel插值器

Kaiser-Bessel函数在成像问题的"网格化"方法中很受欢迎：

$$\psi (\kappa )={\left(\frac{1}{2}\right)}^m{\pi }^{d/2}{\left(\frac{J}{2}\right)}^d{\alpha }^m\frac{\Lambda (z(\kappa ))}{I_m(\alpha )}$$

其中 $I_m$ 表示m阶修正贝塞尔函数。图12比较了（优化的）Kaiser-Bessel插值器、（优化的）高斯钟形插值器和几个最小最大插值器的最大误差。对于这里研究的缩放因子选择（特别是最小二乘拟合方法），相对于Kaiser-Bessel插值器的误差减少为30-50%。

二维和多维扩展

最小最大方法向二维和更高维度的扩展在概念上非常直接。在二维中，我们在两个方向上对二维FFT进行过采样，并为每个期望的频率位置预计算和存储最小最大插值器，使用最近的J×J个样本位置。

对于二维图像，如果使用J₁×J₂的邻域，过采样因子分别为K₁/N₁和K₂/N₂，则矩阵变为Kronecker积：

$${\mathbf{C}}^{(2)}={\mathbf{C}}^{(1)}(N_2)\otimes {\mathbf{C}}^{(1)}(N_1)$$

S(2)=diag{sn2}⊗diag{sn1}\mathbf{S}^{(2)} = \text{diag}\{s_{n_2}\} \otimes \text{diag}\{s_{n_1}\}S(2)=diag{sn2​​}⊗diag{sn1​​}

$${\Lambda }^{(2)}={\Lambda }^{(1)}({\omega }_2)\otimes {\Lambda }^{(1)}({\omega }_1)$$

$${\mathbf{b}}^{(2)}={\mathbf{b}}^{(1)}({\omega }_2)\otimes {\mathbf{b}}^{(1)}({\omega }_1)$$

因此 $\mathbf{T}$ 矩阵变为：

$${\mathbf{T}}_{2D}={\mathbf{T}}_{1D}(J_2,{\mu }_2)\otimes {\mathbf{T}}_{1D}(J_1,{\mu }_1)$$

实际应用：二维示例

为了说明NUFFT方法在实际环境中的准确性，作者考虑了经典的128×128 Shepp-Logan图像。他们在 $[-\pi ,\pi ]\times [-\pi ,\pi ]$ 中生成了10,000个随机频率位置 $({\omega }_m^s)$，并精确计算了二维傅里叶变换（在Matlab的双精度范围内），同时使用J=6和K/N=2的最小最大二维NUFFT方法进行计算。

相对百分比误差定义为：

$$\frac{{\max }_m|\hat{X}({\omega }_m)-X({\omega }_m)|}{{\max }_m|X({\omega }_m)|}\times 100\%$$

使用均匀缩放因子时，误差小于0.14%。使用表II中L=2的优化缩放因子时，误差小于0.011%。当缩放因子基于Kaiser-Bessel缩放因子的最小二乘拟合时，误差小于2.1×10⁻⁴%。这些数量级的误差减少与图3和图12中显示的减少一致，确认了最小化最坏情况误差即使对于实际感兴趣的信号也能带来显著的误差减少。

精确FT方法需要的CPU时间是NUFFT方法的100多倍（由Matlab的tic/toc函数测量）。作为比较，这个问题的经典双线性插值产生6.7%的相对误差。这个大误差就是为什么线性插值对于通过傅里叶方法进行断层重投影不够准确的原因。

---

附录：深入的数学推导

附录A：最小最大插值器的完整推导

从误差表达式开始：

$$\hat{X}({\omega }_m)-X_m=\sum _{j=1}^J{Y}_{[k_m+j{]}_K}{u}_j^{\ast }({\omega }_m)-X({\omega }_m)$$

使用矩阵形式，误差可以写为：

$$\hat{X}({\omega }_m)-X_m={\mathbf{u}}^H({\omega }_m){\mathbf{Y}}_m-{\mathbf{x}}^H{\mathbf{d}}_m$$

其中 ${\mathbf{d}}_m$ 是具有元素 $d_{m,n}=e^{-i{\omega }_{m}n}$ 的向量。

将公式(3)和(12)代入，误差表达式变为：

$$\hat{X}({\omega }_m)-X_m={\mathbf{x}}^H[{\mathbf{u}}^H({\omega }_m){\mathbf{G}}_m-{\mathbf{d}}_m]$$

其中 ${\mathbf{G}}_m$ 是N×J矩阵，元素为：

$$({\mathbf{G}}_m{)}_{n,j}=s_n{e}^{-i\gamma (k_m+j)n}$$

定义以下矩阵和向量：

S=diag{sn},D(ω)=diag{eiωn}\mathbf{S} = \text{diag}\{s_n\}, \quad \mathbf{D}(\omega) = \text{diag}\{e^{i\omega n}\}S=diag{sn​},D(ω)=diag{eiωn}

$$\mathbf{C}\text{ 是 }N\times K\cdot N\text{ 矩阵，}\Lambda (\omega )\text{ 是 }J\times J\text{ 对角矩阵}$$

$$\mathbf{b}(\omega )\text{ 是 }N\text{ 维向量，具有相应的元素}$$

$$D_{nn}(\omega )=e^{i\omega n}{e}^{i\gamma k_0(\omega )(n-n_0)}$$

$$C_{n,j}=\frac{e^{i\gamma j(n-n_0)}}{\sqrt{N}}$$

$${\Lambda }_{jj}(\omega )=e^{-i[\omega -\gamma k_0(\omega )+\gamma j]n_0}$$

$$b_n(\omega )=\frac{e^{i[\omega -\gamma k_0(\omega )](n-n_0)}}{\sqrt{N}}$$

在这种形式下，最小最大问题(11)变为：

$$\underset{\mathbf{u}\in {\mathbb{C}}^N}{\min }\underset{\mathbf{x}\in {\mathbb{C}}^N:\Vert \mathbf{x}{\Vert }_2\le 1}{\max }\sqrt{N}|⟨\mathbf{x},\mathbf{q}(\omega )⟩|$$

通过Cauchy-Schwarz不等式，对于给定频率 $\omega$，最坏情况信号是：

$$\mathbf{x}={\mathbf{q}}^{\ast }(\omega )/\Vert \mathbf{q}(\omega )\Vert$$

将此情况代入最小最大准则并应用相关公式，最小最大问题简化为：

$$\underset{\mathbf{u}(\omega )}{\min }\Vert {\mathbf{S}}^{\ast }\mathbf{C}\Lambda (\omega )\mathbf{u}(\omega )-\mathbf{b}(\omega ){\Vert }^2$$

这个普通最小二乘问题的最小值在 $\omega ={\omega }_m$ 处，其中：

$$\mathbf{u}(\omega )={\mathbf{A}}^{†}(\omega ){\mathbf{C}}^{\ast }\mathbf{Sb}(\omega )$$

其中 $\mathbf{A}={\mathbf{C}}^{\ast }{\mathbf{S}}^{\ast }\mathbf{SC}$。

附录B：高效计算的详细推导

为了有效计算，我们将 $s_n$ 展开为傅里叶级数：

$$s_n=\sum _{l=-L}^L{\alpha }_l{e}^{i\gamma \beta (n-n_0)},n=0,\dots ,N-1$$

将此展开代入 ${\mathbf{C}}_{n,j}^{\ast }$ 的定义：

$${\mathbf{C}}_{n,j}^{\ast }=\sum _{l=-L}^L\sum _{s=-L}^L{\alpha }_l^{\ast }{\alpha }_s{e}^{i\gamma [\beta l+\beta (t-l)](n-n_0)}{u}_{jj}(\omega )$$

经过一系列代数运算，我们得到：

$${\mathbf{C}}_{n,j}^{\ast }=\sum _{l=-L}^L\sum _{s=-L}^L{\alpha }_l^{\ast }{\alpha }_s{\delta }_N(j-l+\beta (t-s))$$

其中 ${\delta }_N(\cdot )$ 是之前定义的Dirichlet类函数。

类似地，对于 $\mathbf{r}(\omega )=\mathbf{D}(\omega )[{\mathbf{S}}^{\ast }\mathbf{C}\Lambda (\omega )\mathbf{u}(\omega )-\mathbf{b}(\omega )]$：

$$r_j(\omega )=\sum _{n=0}^{N-1}{C}_{n,j}^{\ast }{s}_n{b}_n(\omega )=\sum _{t=-L}^L{\alpha }_t\frac{1}{N}\sum _{n=0}^{N-1}{e}^{i\gamma [\omega /\gamma -k_0(\omega )-j+\beta t](n-n_0)}$$

$$=\sum _{t=-L}^L{\alpha }_t{\delta }_N\left(\frac{\omega }{\gamma }-k_0(\omega )-j+\beta t\right)$$

附录C：误差界的严格分析

组合方程(20)和(21)并简化，得到频率 $\omega$ 处的最坏情况误差：

$$\frac{{\mathcal{E}}_{\text{exact}}(\omega )}{\sqrt{N}}=\Vert {\mathbf{S}}^{\ast }[{\mathbf{C}}^{\ast }\mathbf{S}{\mathbf{S}}^{\ast }\mathbf{C}{]}^{-1}{\mathbf{C}}^{\ast }\mathbf{Sb}(\omega )-\mathbf{b}(\omega )\Vert$$

$$=\Vert (\mathbf{I}-\mathbf{Q}{\mathbf{Q}}^{†})\mathbf{b}(\omega )\Vert$$

其中 $\mathbf{Q}$ 在(23)中定义。NUFFT论文中给出的误差界通常被描述为悲观的。相比之下，(40)给出的精确最坏情况误差是可达到的。当然，达到这个最坏情况误差的单位范数信号可能不代表许多感兴趣的问题。

或者，组合(25)和(20)得到：

$$\frac{{\mathcal{E}}_{\text{exact}}(\omega )}{\sqrt{N}}=\sqrt{1-{\mathbf{r}}^{†}(\omega ){\mathbf{T}}^{-1}\mathbf{r}(\omega )}$$

当 $J<10-K/N$ 时，简单形式(41)通常是充分的。对于较大的J，平方根内的减法在数值上是不精确的，所以我们恢复到(40)。

附录D：多维Kronecker积形式

对于d维信号，最小最大插值器的形式变为d个一维插值器的Kronecker积：

$${\mathbf{u}}^{(d)}={\mathbf{u}}^{(1)}({\omega }_d)\otimes {\mathbf{u}}^{(1)}({\omega }_{d-1})\otimes \cdots \otimes {\mathbf{u}}^{(1)}({\omega }_1)$$

相应的误差为：

$${\mathcal{E}}_{d\text{D}}=\prod _{i=1}^d{\mathcal{E}}_{1\text{D}}({\omega }_i)$$

这给出了相对于一维的二维潜在精度"惩罚"的上界。它还表明，良好的一维最小最大插值器的张量积应该在更高维度上工作良好。

附录E：缩放因子优化的数值方法

理想情况下，我们希望使用以下准则选择缩放因子：

$$\underset{\mathbf{s}\in {\mathbb{C}}^N}{\min }\underset{\omega }{\max }\mathcal{E}(\omega )$$

不幸的是，这个优化问题的解析解已被证明是难以捉摸的。对于理想插值器(5)，均匀缩放因子是最优的。直觉上，对于良好的插值器，$s_n$ 应该相当平滑，所以(28)中的低阶展开应该足够。

使用级数展开(28)并表示 ${\mathcal{E}}_{\max }$ 对傅里叶级数系数 $\alpha$ 和 $\beta$ 的依赖，对于给定的L，我们希望求解：

$$\underset{\alpha ,\beta }{\min }{\mathcal{E}}_{\max }(\alpha ,\beta )$$

由于缺乏解析解，作者通过对小L值联合搜索 $\beta$ 和 {αl}\{\alpha_l\}{αl​} 来数值探索这种最小化。例如，对于L=2、J=6和K/N=2的情况，他们在 $[-0.8,0.8]\times [-0.8,0.8]$ 上联合搜索 ${\alpha }_1$ 和 ${\alpha }_2$。最佳 $\beta$ 是0.19，图4绘制了该 $\beta$ 的 ${\mathcal{E}}_{\max }$ 与 ${\alpha }_1$ 的关系。最小值在 ${\alpha }_1=-0.46$ 而不是0，所以显然均匀缩放因子是次优的。