全文第1第2节 - ACCURATE FLOATING-POINT SUMMATION PART I: FAITHFUL ROUNDING

Eloudy

974人浏览 · 2025-08-13 14:14:08

Eloudy · 2025-08-13 14:14:08 发布

【注，全文的一个原则：由于这个理论中仅使用一种工作精度的浮点数，比如仅使用 double 或仅使用 float，因此简称其为 “浮点数”，即某种机器浮点数。】

精确的浮点数求和（第一部分）：忠实的舍入

摘要

给定一个浮点数向量，其精确和为 $s$ 【注，数学精确和】，我们提出一种算法来计算 $s$ 的忠实舍入，即结果是 $s$ 的紧挨着的浮点数邻居之一。若和 $s$ 本身是浮点数【注，计算机能表示的浮点数集合double 类型数的集合 $\mathbb{F}$ ， $s\in \mathbb{F}$ 】，我们证明该算法的结果就是 $s$ 。该算法能去适应求和的条件数，即对于条件数适中的求和，算法速度很快，且计算时间随条件数的对数增长而成比例地缓慢增加。所有结论在存在下溢的情况下仍然成立【注， $f\in[2^{-1022}, 2^{-1021})$ 正规浮点数区间，相邻两个正规浮点数之间的步长为 $2^{-1074}$ ,即 ufp(f) = $2\text{eps}\sigma \\ =2\text{eps}\cdot\text{ufp}(min-normal-floating-point-number)\\ = 2\text{eps}\cdot\text{ufp}(1.0*2^{1-1023}) \\ =2*2^{-53}*2^{-1022}\\ =2^{-1074}$

，如果发生减法，结果可能为 $2^{-1074}$ 或者其几倍数，远小于最小正规数，发生下溢。即，非常靠近0的[2^-1022, 2^-1021)中的小正规数之间相减，结果一般是亚正规数。】，且算法不依赖指数范围。从实测计算时间来看，该算法效率很高，因为它支持良好的指令级并行，既不需要访问尾数或指数等特殊操作，内循环中也没有分支，更不需要额外精度：仅使用工作精度（例如双精度）下的标准浮点加、减、乘运算。算法中使用的某些常数被证明是最优的。

关键词

最高精度求和、忠实的舍入、无误差变换、提炼、高精度、XBLAS、误差分析

AMS 主题分类. 15-04、65G99、65-04

1. 引言与相关工作

我们将提出快速算法来计算浮点数向量的和与点积的高质量近似。由于点积可以无误差地转换为和，因此我们重点研究求和算法。

由于浮点数求和在科学计算中是普遍存在的，相关文献数量庞大，例如 [2, 3, 7, 10, 13, 14, 18, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 36, 37, 39, 40, 41, 42, 46, 47, 48, 49, 50]，这些文献都旨在提高结果的精度。Higham 在 [19] 中专门用一整章讨论求和问题。精确求和或点积算法在数值分析的多个领域有广泛应用，[19, 32] 中可找到出色的综述。

大多数算法是向后稳定的，即计算近似值的相对误差被一个小因子与条件数的乘积所界【注，向后稳定的：输入的舍入误差不会引起结果的剧烈波动；反之，若结果波动剧烈，可以反推出输入也波动剧烈，或者条件数很大】。许多算法 [23, 24, 25, 36, 39, 46, 49, 48]（包括 Kahan、Babuška、Neumaier 等人提出的算法）使用补偿求和，即对单次加法的误差进行某种修正。通常，结果的相对误差被 $\text{eps}$ （相对舍入误差单位）与求和条件数的乘积所界，这是数值分析中一个众所周知的经验法则。

【注，求和条件数： $\kappa = \frac{\sum |x_i|}{|S|}$ ，若向量元素之间正负相消得厉害， $S=\sum x _i$ 绝对值会很小，则会导致 $\kappa$ 的值很大。】

然而，Neumaier 在 [36] 中提出了一种算法，其结果的相对误差被 $\text{eps}^2$ 与求和条件数的乘积所界，这显然与上述经验法则矛盾。该结果的关键在于无误差变换。Neumaier 重新发现了 Dekker 在 [12] 中提出的一种方法（见算法 2.5），该方法将两个浮点数 $a+b$ 的和转换为 $x+y$ 的和，其中 $x$ 是常规浮点近似， $y$ 包含精确误差。令人惊讶的是，若 $|a|\ge|b|$ ，仅需 3 次常规浮点运算即可计算 $x$ 和 $y$ 。近年来，这种无误差变换在许多领域得到应用 [15, 30]。

这种无误差变换被推广到向量，形成所谓的提炼算法（distillation algorithms）。著名的例子包括 Bohlender、Priest、Anderson 和 XBLAS 的工作 [7, 23, 24, 33, 31, 40, 3, 41, 46, 32, 50, 2, 37, 49, 48]。在这类算法中，浮点数向量 $p_i$ 被转换为另一个和相等的向量 ${p'}_i$ ，这一过程称为提炼。在我们最近的论文 [37] 中，我们证明可以将向量 $p_i$ 转换为新向量 $p'_i$ ，使得 $\text{cond}(\sum p'_i)$ (即 $\sum p'_i$ 的条件数，之前提到的 $\kappa = \frac{\sum |x_i|}{|S|}$ ) 基本为 $\text{eps}\cdot \text{cond}(\sum p_i)$ 的条件数，且变换是无误差的，即 $\sum p_i = \sum p'_i$ 。重复这一过程可以为任意条件数的和生成精确近似【注，条件数减小，eps*条件数变小，数值稳定】。

一次提炼后，提炼向量的常规（递归）和的精度相当于在双倍工作精度下计算的结果。这是 XBLAS [32, 2] 或 [37] 中 Sum2 算法的结果精度，对于许多实际应用来说已经足够。然而，结果的相对误差依赖于条件数，例如无法用于计算和的符号。

有少数方法 [34, 39, 7, 40, 41, 46, 13, 14, 50] 可计算与条件数无关的和的精确近似，最终目标是精确和的忠实舍入或四舍五入。本文（第一部分和第二部分）的目标就是这类算法，我们简要概述已知方法。

Bohlender 提出的早期提炼算法之一 [7] 就属于这一范畴，它计算和的四舍五入近似。通常只需几次提炼，但最坏情况下需要 n-1 次（n 为输入向量长度）。后续有 Priest 的双补偿求和 [40, 41]，它对输入数据排序，三次提炼后可保证相对误差最大为 $2\mathbf{eps}$ ，与条件数无关。关于提炼算法的详细综述见 [3]。

其他方法利用浮点数指数范围有限的特性。Malcolm 在 [34] 中提出的早期算法之一将指数范围划分为一系列（重叠的）累加器。求和项 $p_i$ 被划分，使得各部分可无误差地累加到相应的累加器中。累加器的大小和数量根据输入向量长度预先计算。ARPREC [6] 在某种程度上使用类似方法累加部分和。Malcolm 借鉴了 Wolfe [47] 的思想，但只是呈现了其观察，却未加分析。

Malcolm 按降序累加累加器，并分析结果精确到最后一位。另一种方法是 Kulisch [28] 推广的长累加器，其中指数范围由 “相邻” 定点数数组表示，求和项被拆分并累加到相应数组元素，同时传播可能的进位。

Zielke 和 Drygalla [50] 采用了另一种方法。他们将求和项 $p_i$ 相对于 $\mathbf{max}|p_i|$ 拆分为高阶部分和低阶部分。对于小的求和项，高阶部分可能为零。拆分点依赖于维度，且选择为所有高阶部分可无误差相加。重复这一过程直到所有低阶部分为零，从而得到高阶部分的部分和数组 $s_j$ ，满足 $\sum s_j=\sum p_i$ 。接着，通过按升序带进位相加消除部分和 $s_j$ 的重叠部分，最后按降序相加得到的部分和，生成 $\sum p_i$ 的精确近似。

Zielke 和 Drygalla 实质上给出了一段 Matlab 代码（见算法 3.1）；在他们 100 页的德文论文 [50]（关于线性方程组求解）中，仅用 7 行描述该算法，另有 2 行描述一个精度低得多的变体，未给出分析，且排除了下溢情况。

本文借鉴他们的思想，推导并分析一种算法，生成精确和 $s:=\sum p_i$ 的忠实舍入近似 $\text{res}$ 。这意味着在 $\text{res}$ 和 $s$ 之间没有浮点数【注，指计算机表示的浮点数，例如double类型的二进制形式的浮点数】，且当精确和 $s$ 本身是浮点数【注，计算机浮点数】时，可证明 $\text{res}=s$ 。这种算法在数学和数值角度都具有根本意义，应用广泛。例如，它可精确计算残差（求解线性方程组精确解的关键），或严格计算 $\text{sign} (s)$ —— 这在几何谓词计算中至关重要 [10, 20, 45, 9, 27, 8, 14, 38]，其中点积的符号决定点是否在平面上或在哪一侧。

我们在多个方面改进了 Zielke 和 Drygalla 的方法：首先，他们持续提炼(蒸馏)直到低阶部分的向量全为零，若只有一个小量级的求和项，会导致许多不必要的提炼(蒸馏)。我们通过给出判断忠实舍入所需提炼(蒸馏)次数的准则来改进，且证明该准则是最优的；其次，他们通过某种缩放和取整将求和项拆分为高低阶部分，这在现代架构上速度较慢，且糟糕的缩放严重限制了输入向量的指数范围（见第 3 节），我们推导了一种简单快速的替代方法；第三，我们证明前一个高阶部分可无误差地加到后一个上，从而避免消除部分和的重叠部分，因此每一步只需构造一个高阶部分 $t$ 和满足 $s = t + \sum p'_i$ 的剩余向量 $p'_i$ ；第四，无需累加所有部分和，我们证明用常规求和累加低阶部分 $p'_i$ 即可保证忠实舍入，其分析并非易事；最后，所有结果在存在下溢时仍然成立，且消除了对指数范围的严格限制。

我们将证明，该方法的计算量与问题条件数的对数成正比。这是一种近乎理想的情况：简单问题算法速度快，难度增加时速度缓慢下降。

我们的算法速度快。这里的 “快” 不仅指浮点运算次数少，还指实测计算时间短。这意味着避免了取整到整数、访问尾数或指数、分支等特殊操作。计算结果表明，特殊操作可能显著减慢计算。我们的算法仅使用工作精度的浮点加、减、乘运算，无需额外精度。在多数情况下，我们用于计算忠实舍入和的算法甚至比 XBLAS 更快，尽管 XBLAS 的结果质量可能低得多。

本文分为两部分；第一部分结构如下：第 2 节介绍符号并列出一些性质。我们需要大量细致的浮点估计，这些估计常严重依赖位表示和所用浮点算术的定义。这类估计往往繁琐，且有时表述通俗、难以理解。为避免这种情况并确保严谨性，我们发现使用不等式更为方便和严谨。为此，我们开发了一种新工具来描述浮点数、其位表示并处理复杂情况。本节还定义忠实舍入并给出其充分准则。

第 3 节利用该工具开发浮点数向量到一个近似和与某个剩余部分的无误差变换。可估计剩余部分的大小，从而在第 4 节推导具有忠实舍入的求和算法。并证明其停止准则是最优的。我们证明忠实性，尤其包括符号的精确确定。这在存在下溢时仍然成立，且在下溢范围内的计算结果是精确的。我们还估计了依赖于条件数的计算时间。

在本文第二部分 [44] 中，我们定义并研究 K 重忠实舍入（结果由 K 个浮点数组成的向量表示），开发带定向舍入和四舍五入的算法。此外，还给出适用于向量长度接近 $\text{eps}^{-1}$ 的算法，以及一种改进的高效符号确定算法。两部分均给出在 Pentium 4、Itanium 2 和 Athlon 64 处理器上的计算结果。本文（第一、二部分）和 [37] 中提出的所有算法的 Matlab 参考代码可在Institute for Reliable Computing - Overview获取。

与 [37] 和 [44] 一样，本文所有定理、误差分析和证明均由第一作者完成。【注，S.M.RUMP】

2. 基本事实

本节收集分析算法所需的一些基本事实。全文假设无溢出，但允许下溢。所有浮点计算仅使用一种工作精度；例如，我们有时会参考 IEEE 754 双精度。双精度对应 53 bit 精度（包括正规浮点数的一个隐式 bit 1 ）。但需强调，通过替换舍入和下溢单位，以下分析同样适用于其他二进制格式（如 IEEE 754 单精度）。由于我们仅使用一种工作精度的浮点数，因此简称其为 “浮点数”【注，计算机能表示的某个类型的浮点数构成的集合，例如全部 double 二进制能表示的数值的集合】。

浮点数集合记为 $\mathbb{F}$ 【注， $\mathbb{F}$ 包括正规浮点数、亚正规浮点数、零、无穷大（infinity）和非数（NaN）等】， $\mathbb{U}$ 表示亚规格浮点数集合，同时还包含了零和两个最小非零正规浮点数【注，这两个最小的正规浮点数互反，且亚正规浮点数均匀地落于这两个数之间】。单位舍入误差（1.0 到下一个较小浮点数的距离【注，紧挨着1.0 且小于1.0的那个数：1.0-eps=0.999..xyz】）记为 $\text{eps}$ ，下溢单位记为 $\text{eta}$ （即最小正亚正规浮点数）。对于 IEEE 754 双精度， $\text{eps}=2^{-53}$ 【注，参考文章：机器浮点数步长探索】， $\text{eta}=2^{-1074}$ 【注，按照亚正规浮点数计算规则，指数e=-1022； M为第52个尾数 bit 为1其余 bit 为0的尾数值： $M=2^{-52}$ ; $value = (-1)^{s}(0+M)2^{-1022}=2^{-52} 2^{-1022}=2^{-1074}$ 】。则 $\frac{1}{2}\text{eps}^{-1}\text{eta}$ 是最小正正规浮点数【注，double 类型中，最小正正规数二进制构成： 0,00000000001,00...0；共64bits结构, 仅指数最后 bit 含一个1。正规数的 e 至少为1，E= e - 1023。 $value=(-1)^s(1.M)2^{1-1023}=(1.0)2^{-1022}=2^{-1022}$ 】，且对于 $f \in \mathbb{F}$ ，有：

(2.1) $f \in \mathbb{U} \Leftrightarrow 0 \le |f| \le \frac{1}{2}\text{eps}^{-1}\text{eta}$ 【注，U is 亚正规浮点数绝对值+0+两个最小正规数构成的集合】

$\text{fl}(.)$ 表示浮点计算机计算的结果，其中括号内的所有操作均在工作精度下执行。若执行顺序不明确且至关重要，我们会用括号运算符使其唯一。而表达式 $\text{fl}(\sum p_i)$ 本质上意味着求和可按任意顺序进行。我们假设浮点运算采用四舍五入（符合 IEEE 754 算术标准 [1]）。则浮点加和减满足 [19]：

(2.2) $\text{fl}(a\circ b) =(a\circ b)(1+\epsilon) \ \ for \ a,b \in \mathbb{F} \ , \ \circ \in \{+,-\} \ and \ |\epsilon| \le \text{eps}$

【注，加减法的误差限；相对舍入误差单位的由来】

注意，在下溢附近的加和减是精确的 [16]，因此 (2.2) 中无需下溢单位。更准确地说，对于 $a,b \in \mathbb{F}$ ：

(2.3)

$|a+b|\le \text{eps}^{-1}\text{eta} \Rightarrow \text{fl}(a+b)=a+b \ \ \ \ and \\ \\ \text{fl}(a+b) = 0 \Leftrightarrow a=-b$

【注，和在2倍最小正正规浮点数以内的浮点数加法运算，无误差；下溢附近的结果精确】

我们需区分正规浮点数和亚正规浮点数。多位作者 [35, 26, 12] 已指出，浮点数加法的误差始终是浮点数：

(2.4) $a,b \in \mathbb{F} \ \ implies \ \ \delta :=\text{fl}(a+b) -(a+b) \in \mathbb{F}$

【注，浮点数加法的误差是浮点数】

幸运的是，仅需标准浮点数运算即可计算误差项 $\delta$ 。Knuth 在 1969 年提出的以下算法 [26] 是无误差变换的第一个例子。

算法 2.1：两个浮点数和的无误差变换

function [x, y] = TwoSum(a, b)
    x = fl(a + b)
    z = fl(x − a)
    y = fl((a−(x−z))+(b−z))

【注， $a,b,x,y\in \mathbb{F}$ 】

Knuth 算法将任意一对浮点数 $(a,b)$ 转换为新的一对 $(x,y)$ ，满足：

(2.5) $x=\text{fl}(a+b) \ \ and \ \ x+y = a+b$ 【注，Knuth 无误差变换的存在性定理】

【注，Knuth的TwoSum算法是一种精确浮点求和的技巧。它接受两个浮点数a和b作为输入，输出两个浮点数 x 和 y，使得 x 是 a+b 的机器浮点数表示（即 x = fl(a+b)），而 y 是一个修正项，使得 x + y 精确等于 a + b（在实数算术中）。这里的等号 “=” 表示数学上的精确相等，而不是机器做浮点运算的结果。】
这在存在下溢时也成立【注，此时正规浮点数 a，b 符号相反，或者 a，b 本身是亚正规浮点数】。由于 $\mathbb{F}=-\mathbb{F}$ ，可得到减法的无误差变换。

$\text{fl}(\cdot )$ 符号不仅适用于运算操作，也适用于实数本身。对于 $r\in \mathbb{R}$ ， $\text{fl}(r) \in \mathbb{F}$ 是 $r$ 四舍五入到最近浮点数的结果【注，机器浮点数】，遵循 IEEE 754 标准（平局时舍入到偶数【注，M最后一bit为0的那个】）。对于 $f_1,f_2 \in \mathbb{F}$ 和 $r \in \mathbb{R}$ ，舍入的单调性意味着：
(2.6) $f_1\le r \le f_2 \Rightarrow f_1 \le \text{fl}(r) \le f_2$

【注，最近舍入，舍入靠谱，不飘；隐含了 $if \ f_1=f_2, r=f_1=f_2$ 】

(2.7) $f_1 < \text{fl}(r)<f_2 \Rightarrow f_1<r<f_2$

【注，最近舍入】

在数值分析中，结果的精度有时用 “最后一 bit 单位（ulp：unit in the last place）” 衡量。对于以下常需的精细误差估计，ulp 概念的缺点是依赖浮点格式，且在下溢范围需特别注意。

我们引入 “第一 bit 单位（ufp: the unit in the first place）” 或 实数的最高 bit：

(2.8) $0\ne r \in \mathbb{R} \Rightarrow \text{ufp}(r) := 2^{\left \lfloor \text{log}_2|r| \right \rfloor}$

【注，第一 bit 单位计算公式】

【注，向下取整，向着负方向取整； $2^{\left \lfloor \text{log}_2|r| \right \rfloor}$ 的 matlab 实现：

ufp_r = 2^(floor(log2(abs(r))))

比如：r = 11.5 = 8 + 2 + 1 + 0.5，故ufp(11) 为8 】

其中 $\text{ufp}(0):=0$ 。这为描述正规浮点数 $f$ 的 bits 提供了便捷方式：位范围从最高位 $\text{ufp}(f)$ 到 最后一 bit 单位 $2\text{eps}\cdot \text{ufp}(f)$ ，如图 2.1 所示。

【注，ufp(f) 与 ulp(f) 之间差了52个bit的权重】

【注，这里抛弃了 ulp，而仅仅使用 ufp 和 eps 就表示了第一个 bit 单位和最后一 bit 单位。ulp = 2eps*ufp(f), 最后一bit 单位，也就是本阶内步长; 最小正正规浮点数：

$f_{nmin}=\frac{1}{2}\text{eps}^{-1}\text{eta}=2^{-1022}$ ，

那么 $\text{ulp}(f_{nmin})=2\text{eps}\cdot\text{ufp}(f_{nmin})=2*2^{-53}*2^{-1022}=2^{-1074}$ ，

也就是在 $[2^{-1022}, 2^{-1021})$ 这个阶，步长为 $2^{-1074}$ 】

在我们的分析中，常将浮点数视为一个被缩放的整数。对于 $\sigma=2^k, k\in\mathbb{Z}$ ，我们使用集合 $\text{eps}\sigma\mathbb{Z}$ ，可解释为最小正数为 $\text{eps}\sigma$ 的定点数集合。显然， $\mathbb{F} \subseteq \text{eta}\mathbb{Z}$ 【注，机器数学的量子化，普朗克浮点常数为 eta】。注意 (2.8) 与浮点格式无关，也适用于实数： $\text{ufp}(r)$ 是 $r$ 的二进制表示中第一个非零 bit 的值。由此可得：

【注，以 11.5 = 8 + 2 + 1 + 1/2 为例，落在 $\text{ufp}(11.5) = 2^3 = 8$ ; $2*\text{ufp}(11.5) = 16$ ; $2\text{eps}\sigma = 2*2^{-53}*2^3=2^{-49}$ ，是 8.0~16.0 之间的 double 类型数值的步长，参考：机器浮点数步长探索】

(2.9) $0 \ne r \in \mathbb{R} \Rightarrow \text{ufp}(r) \le|r| < 2\text{ufp}(r)$

【注，绝对值不到第一 bit 权重*2；ufp(r) 决定了r处在哪个阶内。】

(2.10) $r,r' \in \mathbb{R}\ and \ \text{ufp}(r)\le |r'| \Rightarrow \text{ufp}(r)\le \text{ufp}(r')$

【注，ufp 主导浮点数 r 的值，等超 50%；r' 值 >= r主值，则r‘ 主值也会是 >= r主值】

我们收集一些性质。对于 $\sigma = 2^k,k\in \mathbb{Z},r\in \mathbb{R}$ ：
(2.11) $\sigma'=2^m,m\in \mathbb{Z} \ and \ \sigma' \ge \sigma \Rightarrow \text{eps}\sigma'\mathbb{Z} \subseteq \text{eps}\sigma \mathbb{Z}$

【注， $\text{eps}\sigma'\mathbb{Z} = \text{eps}(\sigma\cdot2^{m-k}) \mathbb{Z}=\text{eps}\sigma(2^{m-k}\mathbb{Z}) \subseteq \text{eps}\sigma\mathbb{Z}$ 】

【注，ufp 越大，ulp 也越大；大步长的倍数包含于小步长的倍数构成的浮数集合】

(2.12) $f \in \mathbb{F} \ and \ |f|\ge\sigma \Rightarrow \text{ufp}(f)\ge \sigma$

【注，由前提可得，实际上 $|f|\ge \text{ufp}(f) \ge \sigma$ ；且 ufp(f) 阶梯式增减 $2^{-53+k}$ 】

(2.13) $f\in \mathbb{F} \Rightarrow f \in 2\text{eps}\cdot \text{ufp}(f)\mathbb{Z} =2\text{eps}\cdot\sigma\mathbb{Z}$

【注， $2\text{eps}\sigma$ 是 f 最后bit值 ulp(f) ，也是本阶内步长；另外，当 f 绝对值特小时，这个 $2\text{eps}\sigma$ 值会是亚正规浮点数，f 是这个值的整数倍；因为其他 bit 的单位值都是这个 bit 单位值的2幂次倍】

(2.14) $r \in \text{eps}\sigma\mathbb{Z}, |r|\le\sigma\ and \ \text{eps}\sigma \ge \text{eta} \Rightarrow r\in \mathbb{F}$

【注，r 有可能是亚正规数： $\text{eps}=2^{-53}$ ,若 $\sigma=2^{-1021}$ , $\text{eps}\sigma=2^{-53-1021}=2^{-1074}=\text{eta}$ ，且 $z \in \{0,1,2,...,2^{52}-1 \} \subset \mathbb{Z}$ ，那么， $\text{eps}\sigma*z$ 是亚正规浮点数； $z$ 更大的话，进入正规浮点数集合中； $\sigma$ 更大的话， $\text{eps}\sigma$ 也只能是eta 的2的正整数次幂倍，结果 $\text{eps}\sigma*z$ 也更是正规浮点数。因为 $|r|\le \sigma$ , 这意味着 $\mathbb{Z}\le\text{eps}^{-1}=2^{53}$ ; 因为 $\text{eps}\sigma \ge \text{eta}$ ,故 $\sigma \ge \text{eta}\cdot \text{eps}^{-1}=2^{-1074}\cdot 2^{53}=2^{-1021}$ 】

(2.15)

$a,b \in (\mathbb{F}\cap \text{eps}\sigma\mathbb{Z}) \ and \ \\ \delta:=\text{fl}(a+b)-(a+b) \Rightarrow \text{fl}(a+b), a+b, \delta \in \text{eps}\sigma \mathbb{Z}$

【注， $\text{eps}\sigma\mathbb{Z}$ 的封闭性。量子浮点数加减运算封闭。 $\text{eta}\mathbb{Z} =? \mathbb{F}$ 】

(2.16) $a,b \in \mathbb{F}, a\ne 0 \Rightarrow \text{fl}(a+b)\in \text{eps}\cdot\text{ufp(a)}\mathbb{Z}$

【注， $\text{eps}\cdot\text{ufp}(a)$ 是a 步长的一半，“+” 结果不会跌出步长的一半的新步长】

注意 (2.13) 对 $f\in \mathbb{U}$ 也成立。除 (2.16) 外，其他断言均明显成立，(2.16) 稍加思考也可理解，且用我们的工具可轻松严格证明。对于 $a,b\ge 0$ ，由 (2.13) 和 (2.11)，因 $|\text{fl}(a+b)|\ge\text{max}(|a|,|b|)$ ，故断言成立；因此不失一般性，只需证明对于 $a\ge b\ge 0 \ and \ \sigma := \text{ufp}(a)$ ， $\text{fl}(a-b) \in \text{eps}\sigma \mathbb{Z}$ 。若 $\text{ufp}(b)\ge \frac{1}{2}\sigma$ ，则 (2.13) 意味着 $a,b \in \text{eps}\sigma\mathbb{Z}$ ，由 (2.15) 可得断言。若 $\text{ufp}(b)<\frac{1}{2}\sigma$ ，则 $b<\frac{1}{2}\sigma$ ，且 $a\ge \sigma$ 意味着 $a-b>\frac{1}{2}\sigma\in \mathbb{F}$ 。因此 (2.6) 表明 $\text{fl}(a-b)\ge \frac{1}{2}\sigma \in \mathbb{F}$ ，(2.13) 意味着 $\text{fl}(a-b)\in \text{eps}\sigma\mathbb{Z}$ 。

为后续使用，我们再收集一些性质。对于 $r\in \mathbb{R}$ 和 $\tilde{r}=\text{fl}(r)$ ：
(2.17) $\tilde{r}\ne 0 \Rightarrow \text{ufp}(r)\le \text{ufp}(\tilde{r})$

【注，四舍五入导致ufp晋级；但不会因为四舍五入而降级，因为 2^k 具有吸附效应。而且多数情况是=成立，少数为<严格成立】

(2.18)

$\tilde{r}\in \mathbb{F}\setminus \mathbb{U} \Rightarrow |\tilde{r}-r|\le\text{eps}\cdot \text{ufp}(r)\le\text{eps}\cdot \text{ufp}(\tilde{r})$

【注：误差不超过不长的一半，本阶内步长为 $2\text{eps}\cdot\text{ufp}(r)=2\text{eps}\sigma$ ；而 = 成立，是遇到了打平的四舍五入到偶数上的情形】

$\tilde{r}\in \mathbb{U} \Rightarrow |\tilde{r}-r|\le \frac{1}{2}\text{eta}$

【注，本阶内不长为 eta，故误差不超过步长一半】

注意 (2.17) 中严格不等式成立当且仅当 $\tilde{r}$ 是 2 的幂且 $|r|<|\tilde{r}|$ 。

【注， $r=7. \underset{10000 }{99\dots 9} \ , \ \tilde{r}=8.0=2^3$ , ufp 分别是 4和8.】

这些断言由 $\text{fl}(\cdot)$ 的四舍五入性质可得。将 (2.18)、(2.17)、(2.9) 和 (2.3) 应用于浮点加法，对于 $a,b\in \mathbb{F}$ ：
(2.19)

$f=\text{fl}(a+b) \Rightarrow \\ f=a+b+\delta \ with \ |\delta| \le \text{eps}\cdot \text{ufp}(a+b) \le \text{eps}\cdot \text{ufp}(f)\le \text{eps}|f|$

我们常需这种精细误差估计，它比标准估计 (2.2) 好一个因子2。注意下溢时 (2.19) 也成立，因此时 $\delta=0$ ，加法是精确的。以下是浮点数和的大小与误差的精细估计：

(2.20)

$n\text{eps}\le 1, a_i\in \mathbb{F}\ and \ |a_i| \le \sigma \Rightarrow \\ \\| \text{fl}(\sum^n_{i=1}a_i)|\le n\sigma \ and \\ \ \ \ |\text{fl}(\sum^n_{i=1}a_i)-\sum^n_{i=1}a_i| \le \frac{n(n-1)}{2}\text{eps}\sigma$

【注，第一条是有界性，很显然；第二条】

估计 (2.20) 有时可避免不必要的二次项，且对任意求和顺序均成立。两个不等式均可通过归纳法证明：令 $\tilde{s}:=\text{fl}(\sum_{i\ne k} a_i)$ ，则 $|\tilde{s} + a_k|\le n\sigma$ 。若 $n\sigma$ 在溢出范围但 $\text{fl}(\sum a_i)$ 不在，则断言仍成立。否则 $n\text{eps}\le 1$ 意味着 $n\sigma \in \mathbb{F}$ ，(2.6) 证明 $|\text{fl}(\tilde(s+a_k))|\le n\sigma$ 。对于 (2.20) 中的第二个不等式，分两种情况：若 $|\tilde{s}+a_k|=n\sigma$ ，则 $|\tilde{s}|=(n-1)\sigma$ 且 $|a_k|=\sigma$ ，故 $\text{fl}(\tilde{s}+a_k)=\tilde{s}+a_k$ ；若 $|\tilde{s}+a_k|<n\sigma$ ，则 $\text{ufp}(\tilde{s}+a_k) \le (n-1)\sigma$ （因 $\text{ufp}(\cdot)$ 是 2 的幂）。因此 (2.19) 意味着：

$|\text{fl}(\tilde{x}+a_k)-\sum_{i=1}^{n}a_i|\le |\text{fl}(\tilde{s}+a_k)-(\tilde{s}+a_k)|+|\tilde{s}-\sum_{i\ne k}a_i| \\ \ \ \ \ \le\text{eps}\cdot \text{ufp}(\tilde{s}+a_k)+\frac{1}{2}(n-1)(n-2)\text{eps}\sigma \\ \ \ \ \ \le \frac{1}{2}n(n-1)\text{eps}\sigma$

我们注意到该因子可改进为略大于 $n^2/3$ ，但后续无需此结果。

$\text{ufp}$ 概念还提供了浮点加法精确性的简单充分条件。对于 $a,b \in \mathbb{F}$ 和 $\sigma = 2^k,k\in \mathbb{Z}$ ：

(2.21)

$a,b\in \text{eps}\sigma\mathbb{Z} \ and \ |\text{fl}(a+b)|<\sigma \Rightarrow \text{fl}(a+b)=a+b \ and \\ a,b\in\text{eps}\sigma\mathbb{Z} \ and \ |a+b|\le\sigma \Rightarrow \text{fl}(a+b)=a+b$

【注，加法不发生舍入的情况】

只需证明第二部分，因 $\text{fl}(|a+b|)<\sigma$ 和 (2.7) 意味着 $|a+b|<\sigma$ 【注，第一部分便成为第二部分的一个子情况】。为证明第二部分，首先注意 $a+b \in \text{eps}\sigma\mathbb{Z}$ 。由 (2.3)，

若 $|a+b|\le\frac{1}{2}\text{eps}^{-1}\text{eta}$ ，则加法精确；

若 $|a+b|=\sigma$ ，加法也精确。

否则，(2.9) 和 (2.12) 可得 $\sigma>|a+b|\ge \text{ufp}(a+b)\ge \frac{1}{2}\text{eps}^{-1}\text{eta}$ （因 $\frac{1}{2}\text{eps}^{-1}\text{eta}$ 是 2 的幂），故 $\text{eps}\sigma \ge 2\text{eps}\cdot \text{ufp}(a+b)\ge \text{eta}$ ，(2.14) 可完成证明。

Sterbenz 的著名结果 [19, Theorem 2.5] 表明，若同号浮点数 $a,b\in \mathbb{F}$ 相差不大，则减法是精确的。更准确地说，对于 $a,b\ge 0$ ：

(2.22) $\frac{1}{2}a\le b\le 2a \Rightarrow \text{fl}(b-a)=b-a$

用我们的工具不难证明：若 $b\ge a$ ，(2.13) 意味着 $a,b,a-b \in 2\text{eps}\sigma\mathbb{Z}$ （ $\sigma := \text{ufp}(a)$ ）。由假设和 (2.9)， $|b-a|=b-a \le a <2\sigma$ ，(2.21) 证明此部分。若 $b<a$ ，(2.13) 意味着 $a,b,a-b\in 2\text{eps}\sigma\mathbb{Z}$ （ $\sigma := \text{ufp}(b)$ ），类似地 $|b-a|=a-b\le b <2\sigma$ ，(2.21) 完成证明。

对于满足 $\min\{ f:f\in \mathbb{F}\}<r<\max\{ f:f\in \mathbb{F}\}$ 的任意实数 $r$ ，我们定义其浮点前驱和后继：

$\text{pred}(r):=\max\{f\in \mathbb{F}:f<r\} \ \& \ \text{succ}(r):=\min\{f \in \mathbb{F}: r<f\}$

利用 ufp 概念，浮点数的前驱和后继可描述如下（注意 $0\ne |f|=\text{ufp}(f)$ 等价于 $f$ 是 2 的幂）。

引理 2.2：给定非零浮点数 $0 \ne f \in \mathbb{F}$ ，则

$f\notin \mathbb{U} \ and \ |f|\ne \text{ufp}(f) \Rightarrow \text{pred}(f)=f-2\text{eps}\cdot \text{ufp}(f)\ and \ f+2\text{eps}\cdot \text{ufp}(f)=\text{succ}(f),$

$f\notin \mathbb{U}\ and \ f=\text{ufp}(f) \Rightarrow \text{pred}(f)=(1-\text{eps})f \ and \ (1+2\text{eps})f=\text{succ}(f)$

$f\notin \mathbb{U}\ and \ f=-\text{ufp}(f) \Rightarrow \text{pred}(f)=(1+2\text{eps})f \ and \ (1-\text{eps})f=\text{succ}(f)$

$f\in \mathbb{U} \Rightarrow \text{pred}(f)=f-\text{eta}\ and \ f+\text{eta}=\text{succ}(f)$

对于任意 $f\in\mathbb{F}$ （包括下溢情况）：

(2.23) $\text{pred}(f)\le f - \text{eps}\cdot\text{ufp}(f)\le f+\text{eps}\cdot\text{ufp}(f)\le \text{succ}(f)$

【注，f=0时，= 成立；步长为2eps\sigma,所以多数情况下， f+半步长 < succ(f) 】

对于 $f \notin \mathbb{U}$ ：

(2.24) $f-2\text{eps}\cdot \text{ufp}(f)\le \text{pred}(f)<\text{succ}(f)\le f+2\text{eps}\cdot\text{ufp}(f)$

【注，f-2eps.ufp(f) 跨到小一阶的区间的时候，即f是阶界值，第一个\le 中的< 成立？】

注：注意我们在 (2.1) 中将 $\mathbb{U}$ 定义为包含着 $\pm\frac{1}{2}\text{eps}^{-1}\text{eta}$ （最小正规浮点数）。

证明：对于 $f\notin \mathbb{U}$ 且 $|f|\ne\text{ufp}(f)$ ，利用 $\text{ufp}(f)<|f|<2\text{ufp}(f)$ ，且 $|f|=\text{ufp}(f)$ 等价于 $|f|$ 是 2 的幂。其余部分易证。

本文旨在提出一种求和算法，计算精确和的忠实舍入结果。即 [12, 41, 11]：若精确结果是浮点数，则计算结果必须等于该精确结果；否则，必须是精确结果的紧邻浮点邻居之一。

定义 2.3：浮点数 $f\in \mathbb{F}$ 称为实数 $r\in \mathbb{R}$ 的忠实舍入，若
(2.25) $\text{pred}(f)<r<\text{succ}(f)$

记为 $f\in \square (r)$ 。对于 $r\in \mathbb{F}$ ，这意味着 $f=r$ 。

对于一般 $r\notin \mathbb{F}$ ，恰好有两个浮点数满足 $f\in \square(r)$ ，因此与四舍五入相比，最多损失半个位的精度。反之，要计算实数 $r$ 的忠实舍入，只需知道 $r$ 的误差在小范围内即可。相比之下，四舍五入 $\text{fl}(r)$ 最终需要精确知道 $r$ ，特别是当 $r$ 是两个相邻浮点数的中点时，这需要大量且往往不必要的计算量。我们在本文第二部分提出的 $\text{NearSum}$ 算法计算四舍五入结果，其计算时间依赖于求和项的指数范围，而非和的条件数。

相比之下，计算浮点数和的忠实舍入结果的算法 4.5（AccSum）的计算时间与和的条件数的对数成正比，且与求和项的指数范围无关，这与 Malcolm 的方法 [34] 和长累加器 [28] 不同。

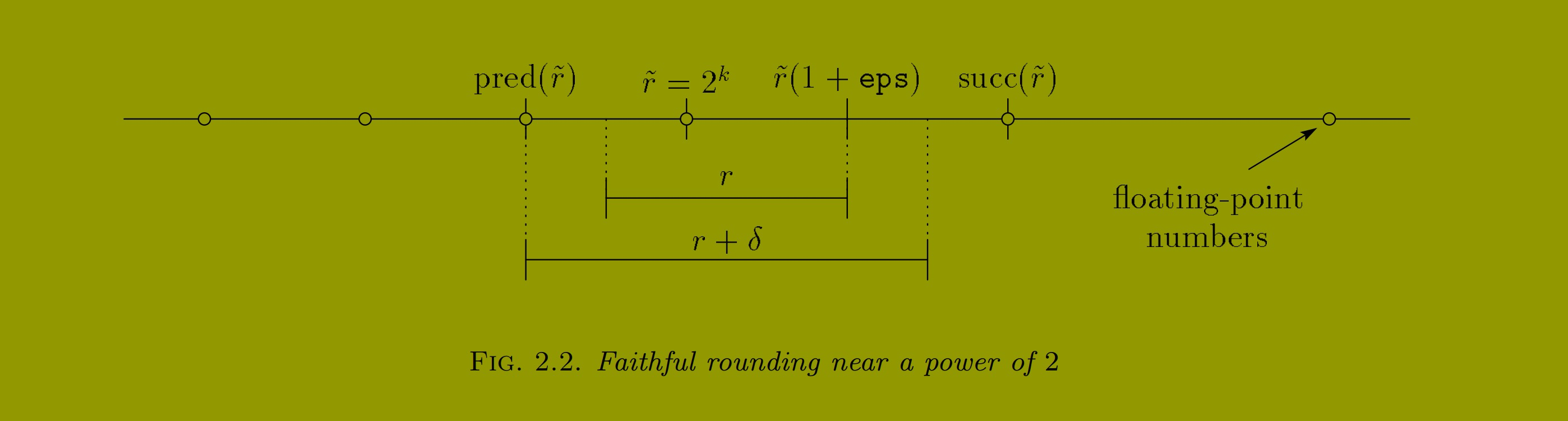
假设 $r+\delta$ 是求和的精确结果，由（实数）近似 $r$ 和误差项 $\delta$ 组成。下面建立 $\delta$ 的条件，以确保 $\text{fl}(r)$ 是 $r+\delta$ 的忠实舍入。关键情况是在 2 的幂处的指数变化，如图 2.2 所示。

引理 2.4：设 $r,\delta\in\mathbb{R}$ 且 $\tilde{r}:=\text{fl}(r)$ 。若 $\tilde{r}\notin \mathbb{U}$ ，假设 $2|\delta|<\text{eps}|\tilde{r}|$ , 且若 $\tilde{r}\in \mathbb{U}$ ，假设 $|\delta|<\frac{1}{2}\text{eta}$ 。则 $\tilde{r}\in\square(r+\delta)$ ，即 $\tilde{r}$ 是 $r+\delta$ 的忠实舍入。

证明：

根据定义 2.3，需证明 $\text{pred}(\tilde{r})<r+\delta<\text{succ}(\tilde{r})$ 。若 $\tilde{r}\in \mathbb{U}$ ，由 (2.18)， $|\tilde{r}-r|\le\frac{1}{2}\text{eta}$ |ṙ−r|≤12eta，因此引理 2.2 可得：

$\text{pred}(\tilde{r})=\tilde{r}-\text{eta}<\tilde{r}-|\tilde{r}-r|+\delta \le r+\delta \le \tilde{r}+|\tilde{r}-r| +\delta < \tilde{r}+\text{eta}=\text{succ}(\tilde{r})$

完成此部分证明。余下处理 $\tilde{r}\notin \mathbb{U}$ 的情况。

由 (2.9)， $\text{ufp}(\tilde(r))\le |\tilde{r}|<2\text{ufp}(\tilde{r})$ ，故 $|\delta|<\text{eps}\cdot \text{ufp}(\tilde{r})$ 。假设 $r\le\tilde{r}$ ，四舍五入意味着

$0\le \tilde{r}-r \le \frac{1}{2}(\tilde{r}-\text{pred}(\tilde{r})) \ and \ |\delta|<\frac{1}{2}(\tilde{r}-\text{pred}(\tilde{r}))$

后者对于 $|\tilde{r}|$ 不是 2 的幂的情况直接由引理 2.2 可得；对于 $|\tilde{r}|$ 是 2 的幂的情况，由 $2|\delta|<\text{eps}|\tilde{r}|=\text{eps}\cdot \text{ufp}(\tilde{r})=\tilde{r}-\text{pred}(\tilde{r})$ 可得。因此 (2.23) 可得：

$\text{pred}(\tilde{r})= \tilde{r}-(\tilde{r}-\text{pred}(\tilde{r})) <\tilde{r}-(\tilde{r}-r) -|\delta| \le r+\delta \le\tilde{r}+\delta < \tilde{r}+\text{eps}\cdot \text{ufp}(\tilde{r}) \le \text{succ}(\tilde{r})$

$r>\tilde{r}$ 的情况类似。

忠实舍入结果满足一些弱序性质。对于 $f,f_1,f_2\in \mathbb{F}$ ， $r\in \mathbb{F}$ 且 $f\in \square(r)$ （即 $f$ 是 $r$ 的忠实舍入），可验证：

(2.26)

$f_1<f<f_2 \Rightarrow f_1<r<f_2 \\f_1<r<f_2 \Rightarrow f_1 \le f \le f_2$

如 (2.4) 所述，浮点加法的误差始终是浮点数。幸运的是，与需要 6 次浮点运算的算法 2.1（TwoSum）相比，在我们的应用中可使用 Dekker [12] 提出的更快算法（仅需 3 次浮点运算）。该计算效率很高，因仅使用标准浮点加和减，无需分支。

算法 2.5：两个浮点数的补偿求和

function [x, y] = FastTwoSum(a, b)
    x = fl(a + b)
    q = fl(x − a)
    y = fl(b − q)

在 Dekker 的原始算法中， $y$ 的计算为 $y=\text{fl}((a-x)+b)$ ，这与算法 2.5 的最后一句等价，因 $\mathbb{F}=-\mathbb{F}$ 且 $\text{fl}(-r)=-\text{fl}(r) \ for \ r\in \mathbb{R}$ 。对于二进制四舍五入浮点算术（如 IEEE 754 算术），Dekker 在 1971 年 [12] 证明，若输入按量级排序（即 | a|≥|b|），则修正项是精确的，即 $x+y=a+b$ 。在 [37] 中，我们指出，在现代计算机上，为消除这一假设而引入分支的做法并非最优，因分支会显著减慢计算。

算法 2.5（FastTwoSum）是将浮点数对 $(a,b)$ 转换为对 $(x,y)$ 的无误差变换。即将提出的算法 4.5（AccSum）也可视为将向量 $p$ 转换为浮点数 $\tau_1,\tau_2$ 和向量 $p'$ 的无误差变换，满足 $\sum p_i=\tau_1+\tau_2+\sum p'_i$ ，且 $\text{res}:= \text{fl}(tau_1+(\tau_2+\sum p'_i))$ 是 $\sum p_i$ 的忠实舍入。为证明这一点，我们需细化算法 2.5 的分析，弱化 $|a|\ge|b|$ 的假设：唯一假设是第一个求和项 $a$ 的所有非零尾数位不小于第二个求和项 $b$ 的最低有效位。

引理 2.6：设 $a,b$ 是浮点数，且 $a\in 2\text{eps}\cdot \text{ufp}(b)\mathbb{Z}$ 。令 $x,y$ 是算法 2.5（FastTwoSum）应用于 $a,b$ 的结果，则
(2.27)

$x+y=a+b, \ x=\text{fl}(a+b)\ and\ |y|\le \text{eps}\cdot\text{ufp}(a+b)\le \text{eps}\cdot \text{ufp}(x)$

此外，
(2.28)

$q=\text{fl}(x-a)=x-a \ and \ y=\text{fl}(b-q)=b-q$

即浮点减法 $x-a$ 和 $b-q$ 是精确的。

注：注意 $|a|\ge|b|$ 意味着 $\text{ufp}(a)\ge\text{ufp}(b)$ ，进而由 (2.13) 和 (2.11)， $a \in 2\text{eps}\cdot \text{ufp}(b) \mathbb{Z}$ ，满足引理 2.6 的假设。

证明：

令 $\text{fl}(a+b)=a+b+\delta$ ，记 $\delta:=2\text{ufp}(b)$ 。注意 $a,b\in \text{eps}\sigma\mathbb{Z}$ 且 $|b|<\sigma$ 。若 $\sigma\le|a|$ ，则 $|b|<|a|$ ，可使用 Dekker 的结果 [12]。否则， $|a+b|<2\sigma$ ，因此 (2.19) 意味着 $|\delta|\le\text{eps}\sigma$ 。实际上，由 (2.15)，要么 $|\delta|=\text{eps}\sigma$ ，要么 $\delta=0$ 。因此 $|x-a|=|b+\delta|\le\text{prd}(\sigma)+\text{eps}\sigma$ ，故 (2.21) 可得 $q=\text{fl}(x-a)=x-a$ ，因此 $y=\text{fl}(b-q)=\text{fl}(-\delta)=-\delta=b-q$ ，证明 (2.28)。因此 $x+y=x-\delta=a+b$ 。 $|y|=|\delta|$ 的估计由 (2.19) 可得，证明完成。□

引理 2.6 也为基于排序的求和算法提供了可能：应用 FastTwoSum 只需 “按指数排序”，复杂度为 $O (n)$ 。

2048 AI社区

有“AI”的1024 = 2048，欢迎大家加入2048 AI社区

更多推荐

适用于制造企业,6种开源 AI 平台对比分析，总有一个适合你

2048 AI社区

宝塔开心版宝塔面板 Linux 企业版 11.0.0【宝塔开心版】一键安装或升级教程

2048 AI社区

4.4单链表专题加应用

另一种思路建立一个新链表Head Tail都赋值NULL，再来一个变量遍历我的原链表pcur指向第一个节点找不为value的节点进行新链表尾插，分两种情况，开始新链表是NULL尾插的话既是头节点也是尾节点，pcur再往后走找到了再往tail->next插入这个节点成为尾戒点如果pcur为value就继续往后走。若pos是第一个节点prev可能一直往下走，出现对空指针解引用的情况，pos是最后一个