一阶条件

本节将对一阶条件（KKT）进行详细讨论，

序列可行方向

定义 设 $x^{\prime }$ 为可行点， { x ( k ) } \{x^{(k)}\} {x(k)} 为可行序列，满足 $x^{(k)}\to x^{\prime }$，且 $\forall k,x^{(k)}\ne x^{\prime }$，则 $x^{(k)}-x^{\prime }$ 为 $x^{\prime }$ 处的可行增量，表示为
$$x^{(k)}-x^{\prime }={\delta }_k{p}^{(k)}$$
其中 $\delta_k > 0 $ 且 ${\delta }_k\to 0$，则 $p^{(k)}$ 是长度固定的向量，称 $p^{(k)}$ 的任一聚点 $p$ 是可行域 $\Omega$ 在 $x^{\prime }$ 处的序列可行方向，全体记为 ${\mathcal{F}}^{\prime }$。

根据定义，一个序列可行方向确定一个可行序列。

例如，可行点 $x^{\prime }=0$，对于 Ω 1 = { x ∈ R 2 : x 2 ≥ x 1 2 } \Omega_1 = \{x\in \mathbb{R}^2:x_2\geq x_1^2\} Ω1​={x∈R2:x2​≥x12​}，则其序列可行方向需要满足 $p_2>0$ 即可。

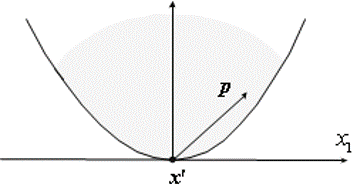
而对于 Ω 2 = { x ∈ R 2 : x 2 = x 1 2 } \Omega_2 = \{x\in \mathbb{R}^2:x_2 = x_1^2\} Ω2​={x∈R2:x2​=x12​}，其序列可行方向需满足
$$p_1\ne 0,p_2=0$$

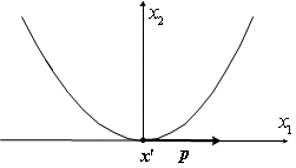
一阶必要条件

不妨设 $f$ 在可行点 $x^{\prime }$ 处的下降方向集为
D ′ = { p ∈ R n ∣ p T g ′ < 0 } D' = \{p\in \mathbb{R}^n|p^Tg' < 0\} D′={p∈Rn∣pTg′<0}

引理 设 $x^{\ast }$ 是约束问题的局部极小点，则在 $x$^* 处没有 序列可行方向是下降方向，即
$${\mathcal{F}}^{\ast }\cap D^{\ast }=\varnothing$$

换言之，上述引理指出若 $x^{\ast }$ 是局部极小点，则目标函数在 $x^{\ast }$ 处沿任一序列可行方向导数非负。

线性化可行方向

然而，集合 ${\mathcal{F}}^{\ast }$ 通常不易计算，考虑另一个易于计算的可行方向集。约束函数 $c_i$ 在 $x^{\prime }$ 处的一阶 Taylor 近似为
$$c_i(x^{\prime }+s)\approx c_i(x^{\prime })+\nabla c_i(x^{\prime }{)}^{T}s$$
定义点 $x^{\prime }$ 处的线性化可行方向是满足
$$\begin{array}{r}{p}^T{a}_i^{\prime }=0,i\in \mathcal{E}\\ p^T{a}_i^{\prime }\le 0,i\in \mathcal{I}\end{array}$$
的非零向量 $p$，所有线性化可行方向形成的集合为 $F^{\prime }$。

显然，如果 ${\mathcal{F}}^{\prime }$ 和 $F^{\prime }$ 相同，将会很方便。

引理 ${\mathcal{F}}^{\prime }\subseteq F^{\prime }$

证明 若 $p\in {\mathcal{F}}^{\prime }$，则存在可行序列 { x ( k ) } \{x^{(k)}\} {x(k)} 满足
$$x^{(k)}-x^{\prime }={\delta }_k{p}^{(k)}$$
其中 ${\delta }_k\to 0,p^{(k)}\to p$。展开约束 $c_i$ 在 $x^{\prime }$ 处的 Taylor 展式
$$c_i(x^{(k)})=c_i(x^{\prime })+{\delta }_k{p}^{(k)}{a}_i^{\prime }+o({\delta }_k)$$
对于 $i\in \mathcal{E}$，有 $c_i(x^{(k)})=c_i(x^{\prime })=0$；对于 $i\in \mathcal{I}$，有 $c_i(x^{(k)})\le c_i(x^{\prime })=0$。因此，有
$$\frac{c_i(x^{(k)})}{{\delta }_k}=\frac{c_i(x^{\prime })}{{\delta }_k}+p^{(k)}{a}_i^{\prime }+\frac{o({\delta }_k)}{{\delta }_k}$$
对于 $k\to \infty$，$p\in F^{\prime }$，引理得证。

令人遗憾的是，$F‘\subseteq {\mathcal{F}}^{\prime }$ 不一定成立。

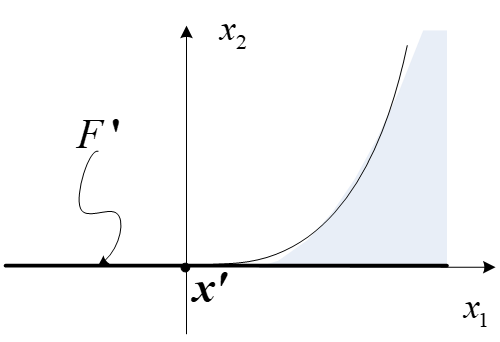
例 定义集合
Ω = { x ∈ R 2 : x 2 ≤ x 1 3 , x 2 ≥ 0 } \Omega = \{x\in\mathbb{R}^2:x_2 \leq x_1^3,x_2\geq 0\} Ω={x∈R2:x2​≤x13​,x2​≥0}
考虑可行点 $x^{\prime }=(0,0{)}^T$，线性化可行方向 $p=(-1,0{)}^T\in F^{\prime }$，显然不存在可行方向收敛于 $p$，即 $p\notin {\mathcal{F}}^{\prime }$。

约束规范

约束规范（constraint quality, CQ）指的是保证 $F‘={\mathcal{F}}^{\prime }$ 的假设条件。需要指出的是，约束规范失效的情况极少出现。

引理 在可行点 $x^{\prime }$ 处，如果条件

(1) LCQ：$c_i(x),i\in {\mathcal{A}}^{\prime }$ 是线性函数，或者

(2) LICQ：$a_i^{\prime },i\in {\mathcal{A}}^{\prime }$ 线性无关

成立，则有 $F‘={\mathcal{F}}^{\prime }$。

Farkas 引理

Farkas 引理 给定 $n$ 维向量 $a_1,a_2,\cdots ,a_m$ 和 $g$，集合
S = { p ∈ R n : p T g < 0 , p T a i ≤ 0 , i = 1 , 2 , ⋯   , m } S = \{ p \in \mathbb{R}^n: p^Tg<0,p^Ta_i \leq 0, i = 1,2,\cdots,m \} S={p∈Rn:pTg<0,pTai​≤0,i=1,2,⋯,m}
是空集当且仅当存在 ${\lambda }_i\ge 0,i=1,2,\cdots ,m$，使得
$$-g=\sum _{i=1}^m{a}_i{\lambda }_i$$

给定 ${\mathbb{R}}^n$ 中的向量 $a_1,a_2,\cdots ,a_m$，令
$$C=\left\{v\in {\mathbb{R}}^n:v=\sum _{i=1}^m{a}_i{\lambda }_i,{\lambda }_i\ge 0\right\}$$
则 $C$ 是一个多面锥，并且是一个闭凸集，

若向量 $a\in C$，则存在超平面分离 $C$ 和 $a$，即存在非零向量 $p$ 使得
$$p^{T}a>0,p^{T}v\le 0,\forall v\in C$$

将引理的必要条件与 Lagrange 乘子建立联系，需要将 Farkas 引理推广到含等式的情况。

推论 给定 ${\mathbb{R}}^n$ 中的向量 $g^{\ast },a_i^{\ast },i\in \mathcal{E},a_i^{\ast },i\in {\mathcal{I}}^{\ast }$，则集合
S = { p ∈ R n : p T g ∗ < 0 , p T a i ∗ = 0 , i ∈ E , p T a i ∗ ≤ 0 , i ∈ I ∗ } S = \{ p \in \mathbb{R}^n: p^Tg^*<0, p^Ta_i^*= 0,i\in \mathcal{E},p^Ta_i^* \leq 0, i \in \mathcal{I}^*\} S={p∈Rn:pTg∗<0,pTai∗​=0,i∈E,pTai∗​≤0,i∈I∗}
是空集当且仅当存在 ${\lambda }_i^{\ast },i\in \mathcal{E},{\lambda }_i^{\ast }\ge 0,i\in {\mathcal{I}}^{\ast }$，使得
$$-g^{\ast }=\sum _{i\in \mathcal{E}}{\lambda }_i^{\ast }{a}_i^{\ast }+\sum _{i\in {\mathcal{I}}^{\ast }}{\lambda }_i^{\ast }{a}_i^{\ast }$$

由上述推论可以证明 KKT 条件。

正则性假设 1：$F^{\ast }\cap D^{\ast }={\mathcal{F}}^{\ast }\in D^{\ast }$

若 $x^{\ast }$ 是局部极小点，且在 $x^{\ast }$ 处正则性假设 1 成立，则
$$F^{\ast }\cap D^{\ast }=\varnothing$$
由 Farkas 引理，知 $\exists {\lambda }_i^{\ast }\in {\mathcal{A}}^{\ast }$，且 ${\lambda }_i^{\ast }\ge 0,i\in {\mathcal{I}}^{\ast }$，使得
$$g^{\ast }+\sum _{i\in \mathcal{E}}{\lambda }_i^{\ast }{a}_i^{\ast }+\sum _{i\in {\mathcal{I}}^{\ast }}{\lambda }_i^{\ast }{a}_i^{\ast }=0$$
当 $i\in \mathcal{I}\backslash {\mathcal{I}}^{\ast }$ 时，有 $c_i(x^{\ast })<0$，此时令 ${\lambda }_i^{\ast }=0$。

KKT 条件

定理（一阶必要条件） 若 $x^{\ast }$ 是局部极小点且 $x^{\ast }$ 处正则性假设
$$F^{\ast }\cap D^{\ast }={\mathcal{F}}^{\ast }\cap D^{\ast }$$
成立，则存在 Lagrange 乘子 ${\lambda }^{\ast }$ 使得 $x^{\ast },{\lambda }^{\ast }$ 满足
$$\begin{array}{rl}{\nabla }_x\mathcal{L}(x^{\ast },{\lambda }^{\ast })& =0\\ c_i(x^{\ast })& =0,i\in \mathcal{E}\\ c_i(x^{\ast })& \le 0,i\in \mathcal{I}\\ {\lambda }_i^{\ast }& \ge 0,i\in \mathcal{I}\\ {\lambda }_i^{\ast }{c}_i(x^{\ast })& =0,i\in \mathcal{I}\end{array}$$

正则性假设是对向量 $a^{\prime }(i\in {\mathcal{A}}^{\prime })$ 的进一步放松。

定理 设 $x^{\ast }$ 是约束问题的局部极小点，且在 $x^{\ast }$ 处LCQ 或者 LICQ成立, 则 $x^{\ast }$ 满足 KKT条件.。

例 考虑问题
$$\begin{array}{rl}\min & x_2\\ \mathrm{s}.\mathrm{t}.& x_2\le x_1^3,x_2\ge 0\end{array}\text{\hspace{1em}(1)}$$
与
$$\begin{array}{rl}\min & x_1\\ \mathrm{s}.\mathrm{t}.& x_2\le x_1^3,x_2\ge 0\end{array}\text{\hspace{1em}(2)}$$
在解 $x^{\ast }=(0,0{)}^T$ 处，易验证 (1) 满足正则性假设，(2) 不满足正则性假设。

参考文献

[1] 刘红英，夏勇，周永生. 数学规划基础，北京，2012.