浅谈各种反演
前言 (chě dàn)反演好神奇啊就像 膜 魔法一样反演在OI界还是一个非常常用的一个东西,觉得还是写个总结好一点前置知识二项式定理 :(证明可通过数学归纳法)正文定义何为反演 ?我是通俗理解为已知 A 求 B为正演, 那已知 B 求 A为反演在OI中一般 A, B为函数,如f(x), g(x)之类的引入先通过一个例题引入有 n 个人站成一排, 编号为1, 2, 3, …, n, 假设编号为i的
前言 (chě dàn)
反演好神奇啊
就像 膜 魔法一样
反演在OI界还是一个非常常用的一个东西,觉得还是写个总结好一点
前置知识
二项式定理 : (证明可通过数学归纳法)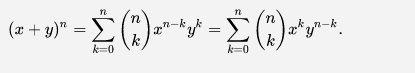
正文
定义
何为反演 ?
我是通俗理解为已知 A 求 B为正演, 那已知 B 求 A为反演
在OI中一般 A, B为函数,如f(x), g(x)之类的
引入
先通过一个例题引入
有 n 个人站成一排, 编号为1, 2, 3, …, n, 假设编号为i的不能站在第i个位置,求可行的方案数 (经典的错排问题)
首先作为一个初中生,当然可以想到容斥
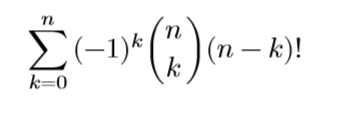
为什么这个公式是成立的
考虑要算m(m >= 1)个人站对的情况, 算0 ~ m-1个人的时候会将当前m个人的方案多算这么多次
既然是负的,加回去就好了,于是容斥公式成立
另一个角度
设 f ( n ) 为 n 个 人 随 便 站 的 方 案 数 , g ( n ) 为 n 个 人 错 排 的 方 案 数 , 我 们 可 以 枚 举 有 几 个 人 站 错 , 可 得 设f(n)为n个人随便站的方案数,g(n)为n个人错排的方案数,我们可以枚举有几个人站错,可得 设f(n)为n个人随便站的方案数,g(n)为n个人错排的方案数,我们可以枚举有几个人站错,可得
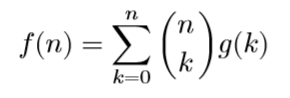
这个就是正演
但是我们好像只知道 f ( n ) f(n) f(n),于是我们需要反演求出 g ( n ) g(n) g(n)
各种反演
开始前先看一些性质
上面设的那个东西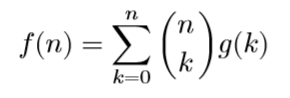
前面推容斥的时候有一步是要用
∑ k = 0 n ( − 1 ) k ( n k ) = ( 1 + ( − 1 ) ) n = 0 n \Large \sum\limits_{k=0}^n(-1)^k \begin{pmatrix} n \\ k \end{pmatrix} = (1 + (-1))^n=0^n k=0∑n(−1)k⎝⎛nk⎠⎞=(1+(−1))n=0n
当n=0时值为1,否则为0
即
∑ k = 0 n ( − 1 ) k ( n k ) = [ n = = 0 ] … … ( 1 ) \Large \sum\limits_{k=0}^n(-1)^k \begin{pmatrix} n \\ k \end{pmatrix} = [n==0]…… (1) k=0∑n(−1)k⎝⎛nk⎠⎞=[n==0]……(1)
首先知道一个显然的东西
g ( n ) = ∑ m = 0 n [ n − m = = 0 ] ( n m ) g ( m ) \large g(n)=\sum\limits_{m=0}^n[n-m==0]\begin{pmatrix} n \\ m \end{pmatrix}g(m) g(n)=m=0∑n[n−m==0](nm)g(m)
前面提到的性质
∑ k = 0 n ( − 1 ) k ( n k ) = [ n = = 0 ] … … ( 1 ) \large \sum\limits_{k=0}^n(-1)^k \begin{pmatrix} n \\ k \end{pmatrix} = [n==0]…… (1) k=0∑n(−1)k(nk)=[n==0]……(1)
把它带进去
g ( n ) = ∑ m = 0 n ∑ k = 0 n − m ( − 1 ) k ( n − m k ) ( n m ) g ( m ) \large g(n)=\sum\limits_{m=0}^n\sum\limits_{k=0}^{n-m}(-1)^k \begin{pmatrix} n-m \\ k \end{pmatrix}\begin{pmatrix} n \\ m \end{pmatrix}g(m) g(n)=m=0∑nk=0∑n−m(−1)k(n−mk)(nm)g(m)
注 意 到 ( n − m k ) ( n m ) 的 意 思 时 从 大 小 为 n 的 集 合 中 先 取 m 个 , 再 从 剩 下 的 中 取 k 个 的 方 案 数 注意到\begin{pmatrix} n-m \\ k \end{pmatrix}\begin{pmatrix} n \\ m \end{pmatrix}的意思时从大小为n的集合中先取m个,再从剩下的中取k个的方案数 注意到(n−mk)(nm)的意思时从大小为n的集合中先取m个,再从剩下的中取k个的方案数 , 和 先 取 k 个 , 再 从 剩 下 的 当 中 取 m 个 的 方 案 数 相 同 ( n − k m ) ( n k ) ,和先取k个,再从剩下的当中取m个的方案数相同\begin{pmatrix} n-k \\ m \end{pmatrix}\begin{pmatrix} n \\ k \end{pmatrix} ,和先取k个,再从剩下的当中取m个的方案数相同(n−km)(nk)
g ( n ) = ∑ m = 0 n ∑ k = 0 n − m ( − 1 ) k ( n − m k ) ( n m ) g ( m ) \ \ \large g(n)=\sum\limits_{m=0}^n\sum\limits_{k=0}^{n-m}(-1)^k \begin{pmatrix} n-m \\ k \end{pmatrix}\begin{pmatrix} n \\ m \end{pmatrix}g(m) g(n)=m=0∑nk=0∑n−m(−1)k(n−mk)(nm)g(m)
= g ( n ) = ∑ m = 0 n ∑ k = 0 n − m ( − 1 ) k ( n − k m ) ( n k ) g ( m ) \large g(n)=\sum\limits_{m=0}^n\sum\limits_{k=0}^{n-m}(-1)^k \begin{pmatrix} n-k \\ m \end{pmatrix}\begin{pmatrix} n \\ k \end{pmatrix}g(m) g(n)=m=0∑nk=0∑n−m(−1)k(n−km)(nk)g(m)
交换求和符号
g ( n ) = ∑ k = 0 n ( − 1 ) k ( n k ) ∑ m = 0 n − k ( n − k m ) g ( m ) \large g(n)=\sum\limits_{k=0}^{n}(-1)^k \begin{pmatrix} n \\ k \end{pmatrix}\sum\limits_{m=0}^{n-k}\begin{pmatrix} n-k \\ m \end{pmatrix}g(m) g(n)=k=0∑n(−1)k(nk)m=0∑n−k(n−km)g(m)
然后我们发现一个很棒的东西
∑ m = 0 n − k ( n − k m ) g ( m ) = f ( n − k ) \large \sum\limits_{m=0}^{n-k}\begin{pmatrix} n-k \\ m \end{pmatrix}g(m) = f(n-k) m=0∑n−k(n−km)g(m)=f(n−k)
所以
g ( n ) = ∑ k = 0 n ( − 1 ) k ( n k ) ∑ m = 0 n − k ( n − k m ) g ( m ) \large g(n)=\sum\limits_{k=0}^{n}(-1)^k \begin{pmatrix} n \\ k \end{pmatrix}\sum\limits_{m=0}^{n-k}\begin{pmatrix} n-k \\ m \end{pmatrix}g(m) g(n)=k=0∑n(−1)k(nk)m=0∑n−k(n−km)g(m)
= ∑ k = 0 n ( − 1 ) k ( n k ) f ( n − k ) \large \ \ \ \ \ \ \ \ = \sum\limits_{k=0}^{n}(-1)^k \begin{pmatrix} n \\ k \end{pmatrix} f(n-k) =k=0∑n(−1)k(nk)f(n−k)
换一下下标
因为 ( n n − k ) = ( n k ) \begin{pmatrix} n \\ n- k \end{pmatrix} = \begin{pmatrix} n \\ k \end{pmatrix} (nn−k)=(nk)
g ( n ) = ∑ k = 0 n ( − 1 ) n − k ( n k ) f ( k ) … … ( 2 ) \large g(n) = \sum\limits_{k=0}^{n}(-1)^{n-k} \begin{pmatrix} n \\ k \end{pmatrix} f(k) …… (2) g(n)=k=0∑n(−1)n−k(nk)f(k)……(2)
二项式反演
先直接给出公式
已知
f ( n ) = ∑ k = 0 n ( n k ) g ( k ) \Large f(n)= \sum\limits_{k=0}^n\begin{pmatrix} n \\ k \end{pmatrix}g(k) f(n)=k=0∑n⎝⎛nk⎠⎞g(k)
可得
g ( n ) = ∑ k = 0 n ( − 1 ) n − k ( n k ) f ( k ) \Large g(n)=\sum\limits_{k=0}^n(-1)^{n-k} \begin{pmatrix} n \\ k \end{pmatrix}f(k) g(n)=k=0∑n(−1)n−k⎝⎛nk⎠⎞f(k)
一般写成
f ( n ) = ∑ k = 0 n ( n k ) g ( k ) ⇔ g ( n ) = ∑ k = 0 n ( − 1 ) n − k ( n k ) f ( k ) \Large f(n)= \sum\limits_{k=0}^n\begin{pmatrix} n \\ k \end{pmatrix}g(k) ⇔ \Large g(n)=\sum\limits_{k=0}^n(-1)^{n-k} \begin{pmatrix} n \\ k \end{pmatrix}f(k) f(n)=k=0∑n⎝⎛nk⎠⎞g(k)⇔g(n)=k=0∑n(−1)n−k⎝⎛nk⎠⎞f(k)
发现和上面的2一样诶
那就不用证了 (笑)
还有另外一个公式
f ( n ) = ∑ k = 0 n ( − 1 ) k ( n k ) g ( k ) ⇔ g ( n ) = ∑ k = 0 n ( − 1 ) k ( n k ) f ( k ) \Large f(n)=\sum\limits_{k=0}^n(-1)^{k} \begin{pmatrix} n \\ k \end{pmatrix}g(k)⇔g(n)=\sum\limits_{k=0}^n(-1)^{k} \begin{pmatrix} n \\ k \end{pmatrix}f(k) f(n)=k=0∑n(−1)k⎝⎛nk⎠⎞g(k)⇔g(n)=k=0∑n(−1)k⎝⎛nk⎠⎞f(k)
这个东西看起来十分对称,非常好记
它的证明也很简单 根据容斥证明就好了
另外有一个更常用的公式
f ( n ) = ∑ k = n m ( k n ) g ( k ) ⇔ g ( n ) = ∑ k = n m ( − 1 ) k − n ( k n ) f ( k ) \Large f(n)= \sum\limits_{k=n}^m\begin{pmatrix} k \\ n \end{pmatrix}g(k) ⇔ \Large g(n)=\sum\limits_{k=n}^m(-1)^{k-n} \begin{pmatrix} k \\ n \end{pmatrix}f(k) f(n)=k=n∑m⎝⎛kn⎠⎞g(k)⇔g(n)=k=n∑m(−1)k−n⎝⎛kn⎠⎞f(k)
证明
把右边的代入左边
f ( n ) = ∑ k = n m ( k n ) g ( k ) f(n)= \sum\limits_{k=n}^m\begin{pmatrix} k \\ n \end{pmatrix}g(k) f(n)=k=n∑m(kn)g(k)
= ∑ k = n m ( k n ) ∑ j = k m ( j k ) ( − 1 ) j − k f ( j ) \ \ \ \ \ \ \ \ \ = \sum\limits_{k=n}^m\begin{pmatrix} k \\ n \end{pmatrix} \sum\limits_{j=k}^m\begin{pmatrix} j \\ k \end{pmatrix}(-1)^{j-k}f(j) =k=n∑m(kn)j=k∑m(jk)(−1)j−kf(j)
= ∑ j = n m f ( j ) ∑ k = n j ( k n ) ( j k ) ( − 1 ) j − k \ \ \ \ \ \ \ \ \ =\sum\limits_{j=n}^m f(j)\sum\limits_{k=n}^j\begin{pmatrix} k \\ n \end{pmatrix}\begin{pmatrix} j \\ k \end{pmatrix}(-1)^{j-k} =j=n∑mf(j)k=n∑j(kn)(jk)(−1)j−k
注 意 到 ( j k ) ( k n ) 的 意 思 时 从 大 小 为 j 的 集 合 中 先 取 k 个 , 再 从 取 的 k 个 中 取 n 个 的 方 案 数 注意到\begin{pmatrix} j \\ k \end{pmatrix}\begin{pmatrix} k \\ n \end{pmatrix}的意思时从大小为j的集合中先取k个,再从取的k个中取n个的方案数 注意到(jk)(kn)的意思时从大小为j的集合中先取k个,再从取的k个中取n个的方案数 , 和 先 取 n 个 , 再 从 剩 下 j − n 的 当 中 取 k − n 个 的 方 案 数 相 同 ( j n ) ( j − n k − n ) ,和先取n个,再从剩下j-n的当中取k-n个的方案数相同\begin{pmatrix} j \\ n \end{pmatrix}\begin{pmatrix} j-n \\ k-n \end{pmatrix} ,和先取n个,再从剩下j−n的当中取k−n个的方案数相同(jn)(j−nk−n)
因 为 ( j − n k − n ) = ( j − n j − n − ( k − n ) ) = ( j − n j − k ) 因为\begin{pmatrix} j-n \\ k-n \end{pmatrix} = \begin{pmatrix} j-n \\ j - n -(k-n) \end{pmatrix}=\begin{pmatrix} j-n \\ j-k \end{pmatrix} 因为(j−nk−n)=(j−nj−n−(k−n))=(j−nj−k)
f ( n ) = ∑ j = n m f ( j ) ∑ k = n j ( j n ) ( j − n j − k ) ( − 1 ) j − k f(n)=\sum\limits_{j=n}^m f(j)\sum\limits_{k=n}^j\begin{pmatrix} j \\ n \end{pmatrix}\begin{pmatrix} j-n \\ j-k \end{pmatrix}(-1)^{j-k} f(n)=j=n∑mf(j)k=n∑j(jn)(j−nj−k)(−1)j−k
= ∑ j = n m ( j n ) f ( j ) ∑ k = n j ( j − n j − k ) ( − 1 ) j − k \ \ \ \ \ \ \ \ \ =\sum\limits_{j=n}^m \begin{pmatrix} j \\ n \end{pmatrix}f(j)\sum\limits_{k=n}^j\begin{pmatrix} j-n \\ j - k \end{pmatrix}(-1)^{j-k} =j=n∑m(jn)f(j)k=n∑j(j−nj−k)(−1)j−k
设 t = j - k
= ∑ j = n m ( j n ) f ( j ) ∑ t = 0 j − n ( j − n t ) ( − 1 ) t \ \ \ \ \ \ \ \ \ =\sum\limits_{j=n}^m \begin{pmatrix} j \\ n \end{pmatrix}f(j)\sum\limits_{t=0}^{j-n}\begin{pmatrix} j-n \\ t \end{pmatrix}(-1)^{t} =j=n∑m(jn)f(j)t=0∑j−n(j−nt)(−1)t
看看右边那个东西,发现是不是有点眼熟
就是性质1
∑ k = 0 n ( − 1 ) k ( n k ) = [ n = = 0 ] … … ( 1 ) \large \sum\limits_{k=0}^n(-1)^k \begin{pmatrix} n \\ k \end{pmatrix} = [n==0]…… (1) k=0∑n(−1)k(nk)=[n==0]……(1)
f ( n ) = ∑ j = n m ( j n ) f ( j ) [ j − n = = 0 ] f(n)=\sum\limits_{j=n}^m \begin{pmatrix} j \\ n \end{pmatrix}f(j)[j-n==0] f(n)=j=n∑m(jn)f(j)[j−n==0]
即
f ( n ) = ∑ j = n m ( j n ) f ( j ) [ j = = n ] f(n)=\sum\limits_{j=n}^m \begin{pmatrix} j \\ n \end{pmatrix}f(j)[j==n] f(n)=j=n∑m(jn)f(j)[j==n]
f ( n ) = ( n n ) f ( n ) [ n = = n ] f(n)=\begin{pmatrix} n \\ n \end{pmatrix}f(n)[n==n] f(n)=(nn)f(n)[n==n]
f ( n ) = f ( n ) f(n)=f(n) f(n)=f(n)
得证
一般的用法:
f(n)为先钦定n个,然后剩下随便搞的方案数(肯定会算重复) (不是简单的后缀和,而是先钦定n个的所有情况,然后剩下随便搞的和)
g(n)为恰好n个
显然
f ( n ) = ∑ k = n m ( k n ) g ( k ) \Large f(n)= \sum\limits_{k=n}^m\begin{pmatrix} k \\ n \end{pmatrix}g(k) f(n)=k=n∑m⎝⎛kn⎠⎞g(k)
一般 f ( n ) f(n) f(n)是很容易算的,那么
g ( n ) = ∑ k = n m ( − 1 ) k − n ( k n ) f ( k ) \Large g(n)=\sum\limits_{k=n}^m(-1)^{k-n} \begin{pmatrix} k \\ n \end{pmatrix}f(k) g(n)=k=n∑m(−1)k−n⎝⎛kn⎠⎞f(k)
莫比乌斯反演
f ( n ) = ∑ d ∣ n g ( d ) ⇔ g ( n ) = ∑ d ∣ n μ ( d ) f ( n / d ) \Large f(n)=\sum\limits_{d|n}g(d)⇔g(n)=\sum\limits_{d|n}\mu (d)f(n/d) f(n)=d∣n∑g(d)⇔g(n)=d∣n∑μ(d)f(n/d)
前置知识
首先要知道 μ \mu μ是个什么函数
若 d = 1 , μ ( d ) = 1 若d = 1, \mu(d) = 1 若d=1,μ(d)=1
若 d = p 1 ∗ p 2 ∗ p 3 ∗ . . . . ∗ p k , 其 中 p 为 质 数 且 互 不 相 同 , 那 么 μ ( d ) = ( − 1 ) k 若d=p_1 * p_2 * p_3 * .... * p_k, 其中p为质数且互不相同,那么 \mu(d) = (-1)^k 若d=p1∗p2∗p3∗....∗pk,其中p为质数且互不相同,那么μ(d)=(−1)k
其 他 情 况 μ ( d ) = 0 其他情况 \mu(d) = 0 其他情况μ(d)=0
μ \mu μ 的一些性质
首先它是一个积性函数
就是若 a, b互质
则满足 μ ( a b ) = μ ( a ) μ ( b ) \large \mu(ab)=\mu(a)\mu(b) μ(ab)=μ(a)μ(b)
证明很显然啊
然后就可以线性筛了
还有一个很重要的性质
∑ d ∣ n μ ( d ) = [ n = = 1 ] \large \sum\limits_{d|n}\mu(d) =[n==1] d∣n∑μ(d)=[n==1]
这个证明也很显然,先把n质因数分解,去掉重复的质因数
假设为 p 1 , p 2 , . . . . , p m p_1,p_2, ...., p_m p1,p2,....,pm
上面那条式子就等价于 ∑ k = 0 m ( − 1 ) k ( m k ) \sum\limits_{k=0}^m(-1)^k\begin{pmatrix} m \\ k \end{pmatrix} k=0∑m(−1)k(mk)
这条式子是不是有点熟悉, 就是上面的性质1
∑ k = 0 n ( − 1 ) k ( n k ) = [ n = = 0 ] … … ( 1 ) \sum\limits_{k=0}^n(-1)^k \begin{pmatrix} n \\ k \end{pmatrix} = [n==0]…… (1) k=0∑n(−1)k(nk)=[n==0]……(1)
所以
∑ k = 0 m ( − 1 ) k ( m k ) = [ m = = 0 ] \sum\limits_{k=0}^m(-1)^k\begin{pmatrix} m \\ k \end{pmatrix}=[m==0] k=0∑m(−1)k(mk)=[m==0]
m = = 0 的 时 候 n 只 能 为 1 m==0的时候n只能为1 m==0的时候n只能为1
所以成立
证明
让我们回忆我们证明二项式反演的时候干了什么?
找了个n=0时才为1的东西,然后搞了个显然的东西,把前一个带入后面一个就搞出了反演
类似的我们可以搞一搞
∑ d ∣ n μ ( d ) = [ n = = 1 ] \large \sum\limits_{d|n}\mu(d) =[n==1] d∣n∑μ(d)=[n==1]
显然的
g ( n ) = ∑ m ∣ n [ n m = = 1 ] g ( m ) \large g(n)=\sum\limits_{m|n}[\frac{n}{m}==1]g(m) g(n)=m∣n∑[mn==1]g(m)
把上面的代入下面
g ( n ) = ∑ m ∣ n ∑ d ∣ n m μ ( d ) g ( m ) g(n)=\sum\limits_{m|n}\sum\limits_{d|\frac{n}{m}}\mu(d) g(m) g(n)=m∣n∑d∣mn∑μ(d)g(m)
注意到 d ∣ n m 就 是 m d ∣ n 和 m ∣ n d d|\frac{n}{m}就是md|n和m|\frac{n}{d} d∣mn就是md∣n和m∣dn是等价的
所以
g ( n ) = ∑ m ∣ n ∑ m ∣ n d μ ( d ) g ( m ) g(n)=\sum\limits_{m|n}\sum\limits_{m|\frac{n}{d}}\mu(d) g(m) g(n)=m∣n∑m∣dn∑μ(d)g(m)
同样交换求和符号
g ( n ) = ∑ d ∣ n μ ( d ) ∑ m ∣ n d g ( m ) g(n)=\sum\limits_{d|n}\mu(d) \sum\limits_{m|\frac{n}{d}} g(m) g(n)=d∣n∑μ(d)m∣dn∑g(m)
右边那个东西是不是有点熟悉
就是 f ( n ) = ∑ d ∣ n g ( d ) f(n)=\sum\limits_{d|n}g(d) f(n)=d∣n∑g(d)
所以
g ( n ) = ∑ d ∣ n μ ( d ) f ( n / d ) g(n) =\sum\limits_{d|n}\mu(d)f(n/d) g(n)=d∣n∑μ(d)f(n/d)
证毕
另一种形式
f ( n ) = ∑ n ∣ d g ( d ) ⇔ g ( n ) = ∑ n ∣ d μ ( d / n ) f ( d ) \Large f(n)=\sum\limits_{n|d}g(d)⇔g(n)=\sum\limits_{n|d}\mu (d/n)f(d) f(n)=n∣d∑g(d)⇔g(n)=n∣d∑μ(d/n)f(d)
类比二项式反演的证明
把右边的代入左边
f ( n ) = ∑ n ∣ d g ( d ) f(n)=\sum\limits_{n|d}g(d) f(n)=n∣d∑g(d)
= ∑ n ∣ d ∑ d ∣ m μ ( m / d ) f ( m ) \ \ \ \ \ \ \ \ \ =\sum\limits_{n|d}\sum\limits_{d|m}\mu (m/d)f(m) =n∣d∑d∣m∑μ(m/d)f(m)
= ∑ n ∣ m ∑ t ∣ m n m / n μ ( m / t n ) f ( m ) \ \ \ \ \ \ \ \ \ =\sum\limits_{n|m}\sum\limits_{t|\frac{m}{n}}^{m/n}\mu (m/tn)f(m) =n∣m∑t∣nm∑m/nμ(m/tn)f(m)
设 m / n = T m/n=T m/n=T
f ( n ) = ∑ n ∣ m ∑ t ∣ m n T μ ( T / t ) f ( m ) f(n) =\sum\limits_{n|m}\sum\limits_{t|\frac{m}{n}}^{T}\mu (T/t)f(m) f(n)=n∣m∑t∣nm∑Tμ(T/t)f(m)
= ∑ n ∣ m f ( m ) ∑ t ∣ T T μ ( T / t ) \ \ \ \ \ \ \ \ \ =\sum\limits_{n|m}f(m)\sum\limits_{t|T}^{T}\mu (T/t) =n∣m∑f(m)t∣T∑Tμ(T/t)
可以很容易发现
∑ t ∣ T T μ ( T / t ) = ∑ t ∣ T T μ ( t ) \sum\limits_{t|T}^{T}\mu (T/t)=\sum\limits_{t|T}^{T}\mu (t) t∣T∑Tμ(T/t)=t∣T∑Tμ(t)
f ( n ) = ∑ n ∣ m f ( m ) ∑ t ∣ T T μ ( t ) f(n) =\sum\limits_{n|m}f(m)\sum\limits_{t|T}^{T}\mu (t) f(n)=n∣m∑f(m)t∣T∑Tμ(t)
右边那个东西是不是又很熟悉
∑ d ∣ n μ ( d ) = [ n = = 1 ] \large \sum\limits_{d|n}\mu(d) =[n==1] d∣n∑μ(d)=[n==1]
就是这个东西
所以
f ( n ) = ∑ n ∣ m f ( m ) [ T = = 1 ] f(n) =\sum\limits_{n|m}f(m)[T==1] f(n)=n∣m∑f(m)[T==1]
= ∑ n ∣ m f ( m ) [ m / n = = 1 ] \ \ \ \ \ \ \ \ \ =\sum\limits_{n|m}f(m)[m/n==1] =n∣m∑f(m)[m/n==1]
= ∑ n ∣ m f ( m ) [ m = = n ] \ \ \ \ \ \ \ \ \ =\sum\limits_{n|m}f(m)[m==n] =n∣m∑f(m)[m==n]
= f ( n ) \ \ \ \ \ \ \ \ \ =f(n) =f(n)
证毕
一般用法
设g(n)为gcd(x, y) == n的对数
设f(n)为n | gcd(x,y)的对数 (1 <= x <= N, 1 <= y <= M)
显然满足
f ( n ) = ∑ n ∣ d g ( d ) \large f(n)=\sum\limits_{n|d}g(d) f(n)=n∣d∑g(d)
一般f(n)很容易算就是
f ( n ) = ⌊ N n ⌋ × ⌊ M n ⌋ \large f(n)= \lfloor\frac{N}{n}\rfloor \times\lfloor\frac{M}{n}\rfloor f(n)=⌊nN⌋×⌊nM⌋
那么显然
g ( n ) = ∑ n ∣ d μ ( d / n ) f ( d ) \large g(n)=\sum\limits_{n|d}\mu (d/n)f(d) g(n)=n∣d∑μ(d/n)f(d)
= ∑ n ∣ d μ ( d / n ) ⌊ N d ⌋ × ⌊ M d ⌋ \large \ \ \ \ \ \ \ \ \ = \sum\limits_{n|d}\mu (d/n) \lfloor\frac{N}{d}\rfloor \times\lfloor\frac{M}{d}\rfloor =n∣d∑μ(d/n)⌊dN⌋×⌊dM⌋
做题前还有一个东西必须要掌握 : 整除分块
有些题推出来的式子你会发现有整除,然而对于一个数除以一段连续的数得到的结果是相同的
举个例子
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| ⌊ 10 / i ⌋ \lfloor 10/i\rfloor ⌊10/i⌋ | 10 | 5 | 3 | 2 | 2 | 1 | 1 |
那已知左端点,如何求右端点?
右端点 r = n / ( n / l ) r=n/(n/l) r=n/(n/l)
反正也不难记,先记着,后面有时间再证明(flag)
可见连续一段是相等的
for(int l=1,r;l<=n;l=r+1) {
r= n / (n / l);
计算l ~ r这段的结果
}
对于两个数 n , m n,m n,m的类比做一下就好了
for(int l = 1, r = 0; l <= n; l = r + 1) {
r = min(n / (n / l), m / (m / l));
计算l ~ r这段的结果
}
两年前自己写的关于莫比乌斯反演的垃圾 : 莫比乌斯反演(懵逼钨丝繁衍)
里面有几道题
子集反演
就是裸的容斥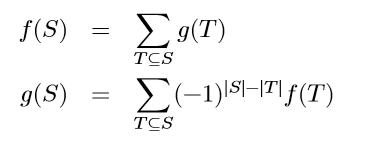
FWT
之前写过 浅谈FWT
子集卷积
同上,数组多开一维记一下集合大小就好了
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)